Предмет: Алгебра,
автор: diss111dd
НУЖНА СРОЧНАЯ ПОМОЩЬ, ДАЮ ВСЕ БАЛЛЫ
Приложения:
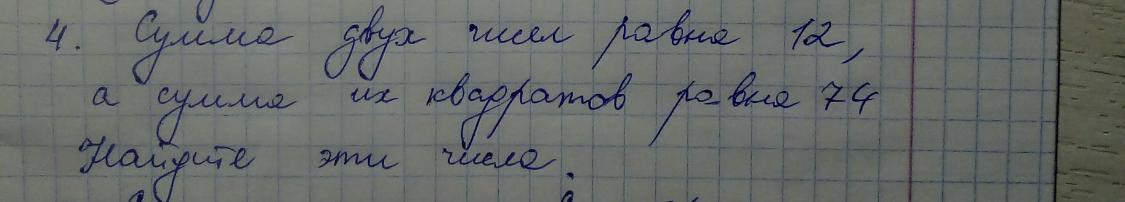
Ответы
Автор ответа:
0
Відповідь:
a+b=12
a²+b²=74
b=12-a
a²+(12-a)²=74
a²+144-24a+a²=74;
2a²-24a+70=0
a²-12a+35=0
a₁=5 или a₂=7
b₁=12-5=7 b₂=12-7=5
Ответ: 5 и 7
Автор ответа:
0
Ответ:
(7;5)
(5;7)
Объяснение:
⇒
⇒ x(12 - x) = 35
x(12 - x) = 35
Тогда пара чисел (6;6) - не является решением системы.
Тогда пара чисел (7;5) - является решением системы.
А так система симметрична, то пара чисел (7;5) тоже является решением системы.
Похожие вопросы
Предмет: Русский язык,
автор: kirichenkoanast
Предмет: Английский язык,
автор: pomogaika11232313
Предмет: Другие предметы,
автор: элина49
Предмет: Геометрия,
автор: vikamart2000