Предмет: Геометрия,
автор: sorax17
Помогите пожалуйста, очень надо
Приложения:
Ответы
Автор ответа:
1
Ответ:
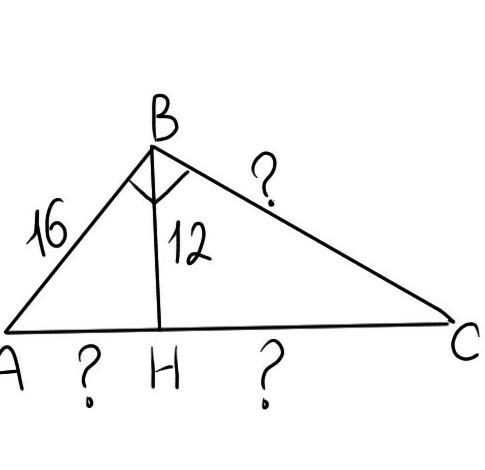
Рассмотрим треугольник АВН:
найдем угол АН за теоремой Пифагора:
16²-12²=112
√112=4√7
tgA = 12/4√7=3/√7
Рассмотрим весь треугольник.
tgA = BC ÷ AB
BC = tgA × AB
BC = 3/√7 ×16 = 48√7/7
что-то страшный ответ вышел
уж и сам засомневался.
sorax17:
Герой, спасибо
Автор ответа:
0
Ответ:
Объяснение:
АН найдём из теоремы Пифагора:
Далее из метрических соотношений в прямоугольном треугольнике:
ВС найдём по теореме Пифагора:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Ser20051
Предмет: Русский язык,
автор: olesyanik1
Предмет: Английский язык,
автор: Кошачийвождь
Предмет: Русский язык,
автор: gasga111men
Предмет: ОБЖ,
автор: Аноним