Предмет: Алгебра,
автор: Аноним
Найти общее решение дифференциальных уравнений. Помогите пожалуйста !
Приложения:
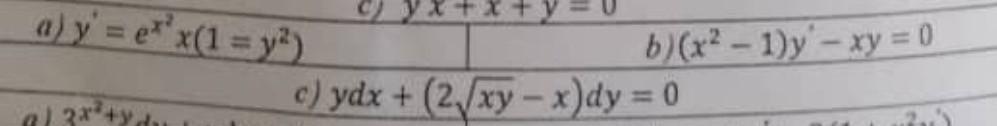
Miroslava227:
в букве а там два равно
Ответы
Автор ответа:
1
Ответ:
a)
сразу сократим 1/2
общее решение
б)
общее решение
в)
общее решение
Похожие вопросы
Предмет: Қазақ тiлi,
автор: FactoryDash
Предмет: Русский язык,
автор: kiss180186
Предмет: Русский язык,
автор: Вован1988
Предмет: Литература,
автор: vayraakyheva
Предмет: Окружающий мир,
автор: esareff