Предмет: Алгебра,
автор: Аноним
Помогите даю 100 бал Найти частное решение дифференциального уравнения и вычислить значение полученной фукции у=ф(x) при Х=Хос точностью до двух цифр после запятой.
Приложения:
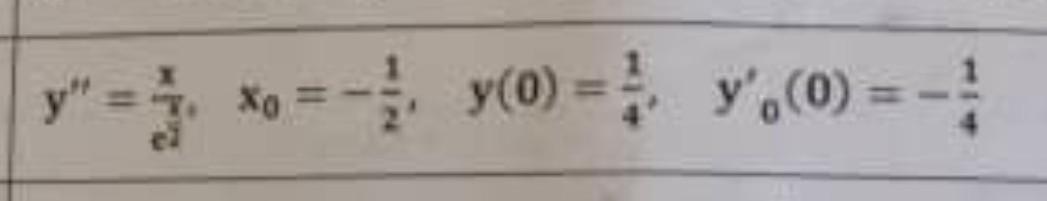
Miroslava227:
в знаменателе у е степень х/2 ?
Ответы
Автор ответа:
0
Ответ:
По частям:
общее решение
частное решение
При
Ответ: 0,35
Похожие вопросы
Предмет: Русский язык,
автор: дашенька20042
Предмет: Русский язык,
автор: Doooooogwooolf12345
Предмет: Английский язык,
автор: katyushaafanas
Предмет: Литература,
автор: льошик123
Предмет: Литература,
автор: ПОМОГИТе0009