Предмет: Алгебра,
автор: kiragoh012
Помогите пожалуйста сделать
Приложения:
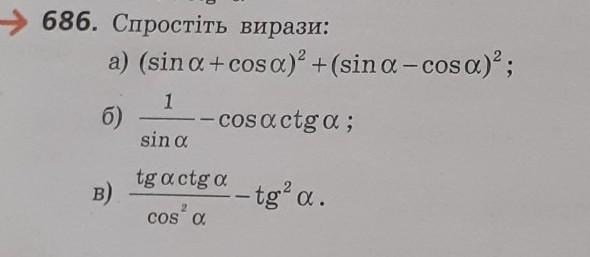
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: вероника164
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: мила1078
Предмет: Алгебра,
автор: Klola
Предмет: Алгебра,
автор: ХолявкаТвоя