Предмет: Математика,
автор: daniksafonov88
Помогите найти площадь
Приложения:
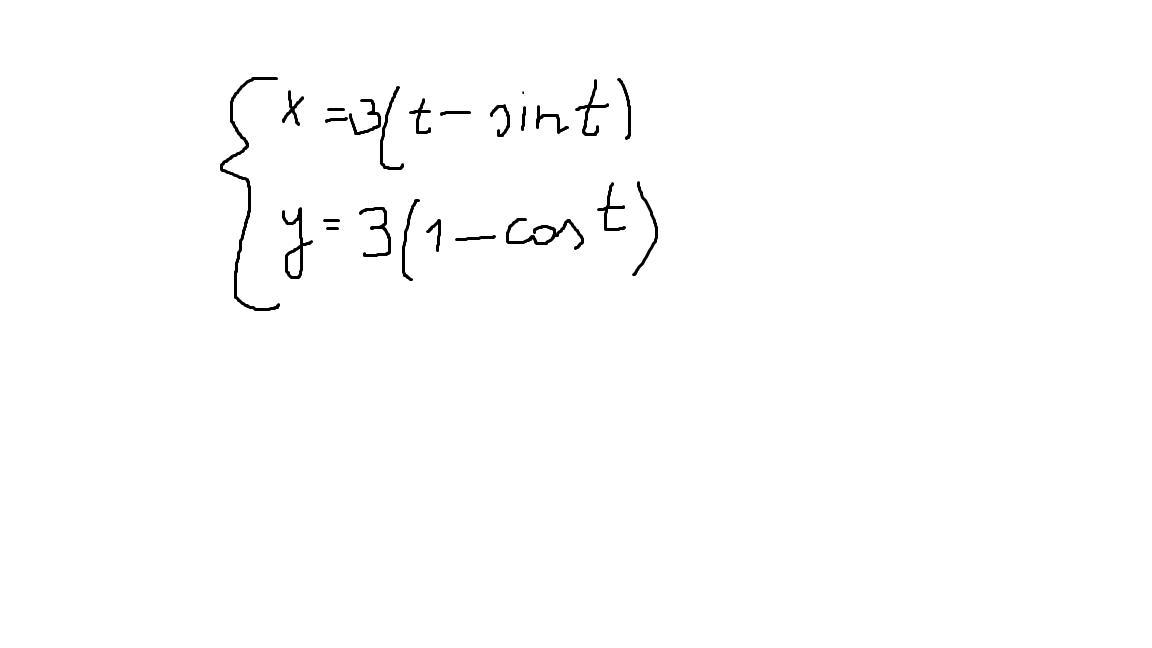
pushpull:
для этой циклоиды не даны отграничения по t. какую площадь искать?
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
здесь у нас циклоида
я найду площадь одной "арки" циклоиды, а там смотрите дальше. все эти арки равноплощадны
рисуем график и смотрим пределы интегрирования.
хотя можно и аналитически
если период циклоиды равен 2π,
то период циклоиды будет равен 6π
формула площади для параметрически заданных функций
x'(t) = 3(1-cost)
t₁ = 0 t₂ = 6π
итого считаем интеграл
Приложения:
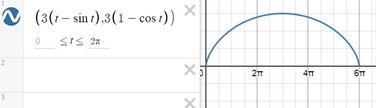
ответ будет 27pi
Похожие вопросы
Предмет: Русский язык,
автор: lediboss
Предмет: Русский язык,
автор: окп1
Предмет: Русский язык,
автор: lediboss
Предмет: Английский язык,
автор: Krista50
Предмет: Алгебра,
автор: nikitamutovkinp6hzp9