Предмет: Алгебра,
автор: tabenter1
Найти sinα, tgα и ctgα, если для острого угла α: ... ДАЛЬШЕ СМОТРЕТЬ ВЛОЖЕНИЕ!!! Сделать все номера которые там есть... с решением, ответом, пожалуйста, срочно! =)
Приложения:

Ответы
Автор ответа:
0
1) по основному тригонометрич. тождеству  ,
,
значит что (с учетом что угол острый значит косинус и синус положительгные)



2)

3)
значит что (с учетом что угол острый значит косинус и синус положительгные)
2)
3)
Автор ответа:
0
К сожалению, только 2 номера. Я очень спешу.
Приложения:

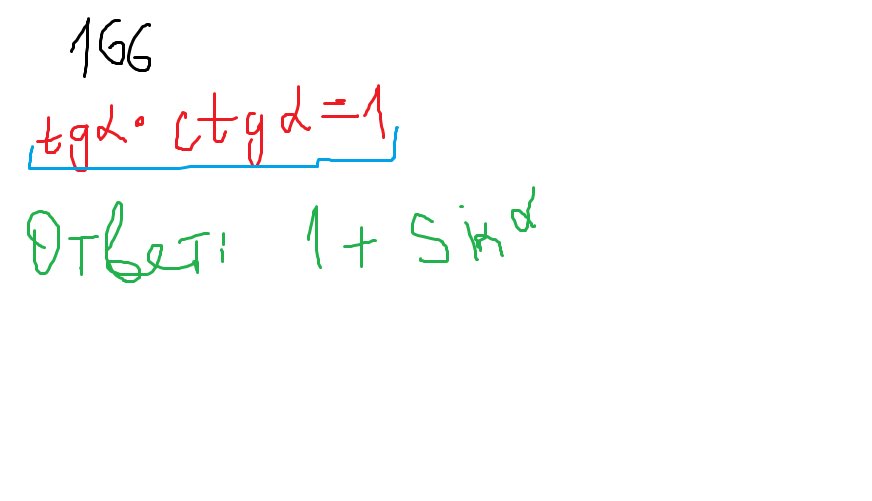
Похожие вопросы
Предмет: Русский язык,
автор: kvan7710olga
Предмет: Қазақ тiлi,
автор: danialalimbekov
Предмет: История,
автор: Tim20089
Предмет: Алгебра,
автор: Ruslan9586
Предмет: Физика,
автор: prettukitten