Question

Знайдіть радіус кола, описаного навколо рівнобедреного трикутника з основою 24 см, якщо висота, проведена до неї, дорівнює 8 см. Де лежить центр кола?

Answer 1

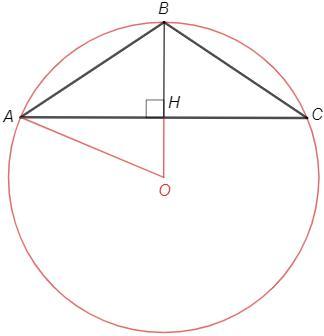
AC=24, BH=8

ABC - равнобедренный, BH - высота и медиана

AH =AC/2 =12

BC =AB =√(AH^2 +BH^2) =4√(9+4) =4√13 (т Пифагора)

sinA =BH/AB =2/√13

BC/sinA =2R (т синусов) => R =4√13*√13/2*2 =13 (см)

AB^2 +BC^2 =16*13*2 < AC^2 => ∠ABC >90

В тупоугольном треугольнике центр описанной окружности лежит вне треугольника.

Проверка: OH=13-8=5, треугольник AOH со сторонами 5, 12, 13