Предмет: Математика,
автор: dshelenkov2004
помогите решить пожалуйста ОчЕнь срочно
Приложения:
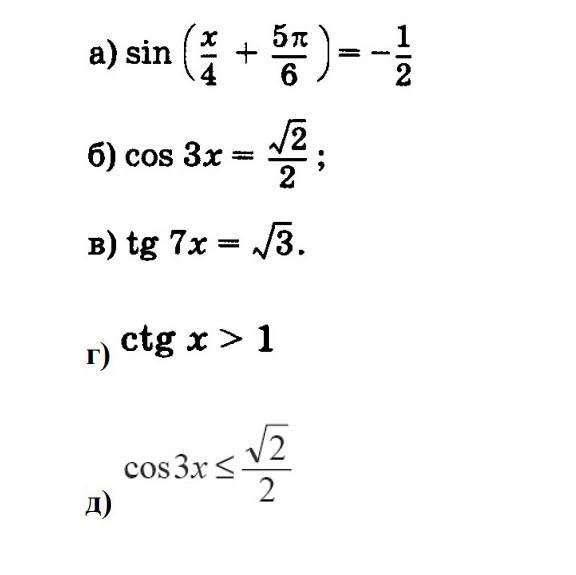
Ответы
Автор ответа:
1
Ответ:
a)
б)
в)
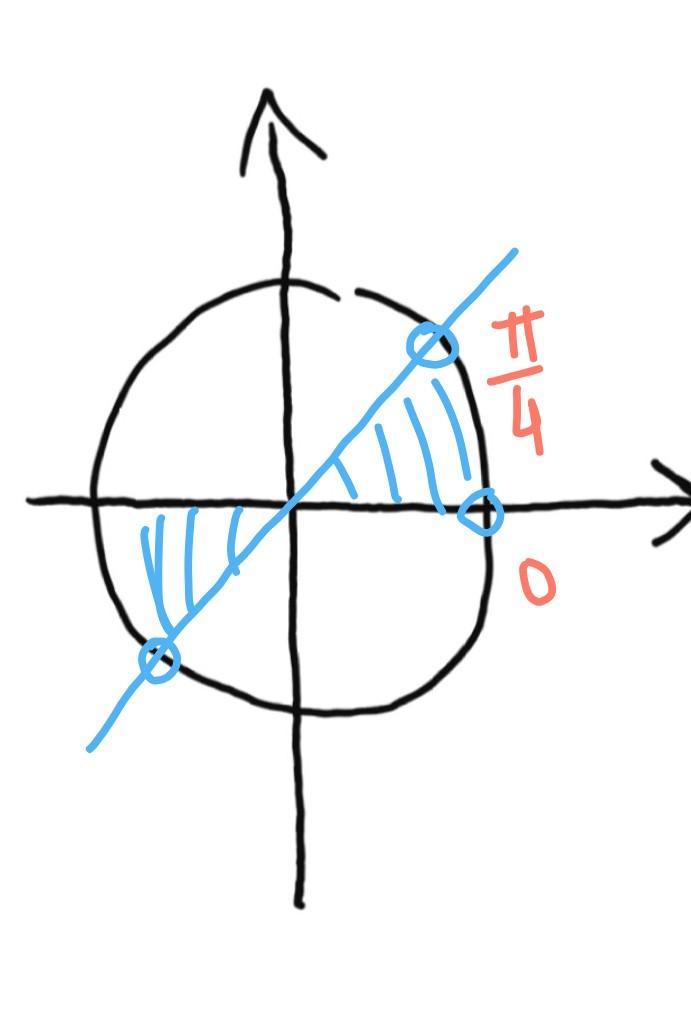
г)
рисунок1
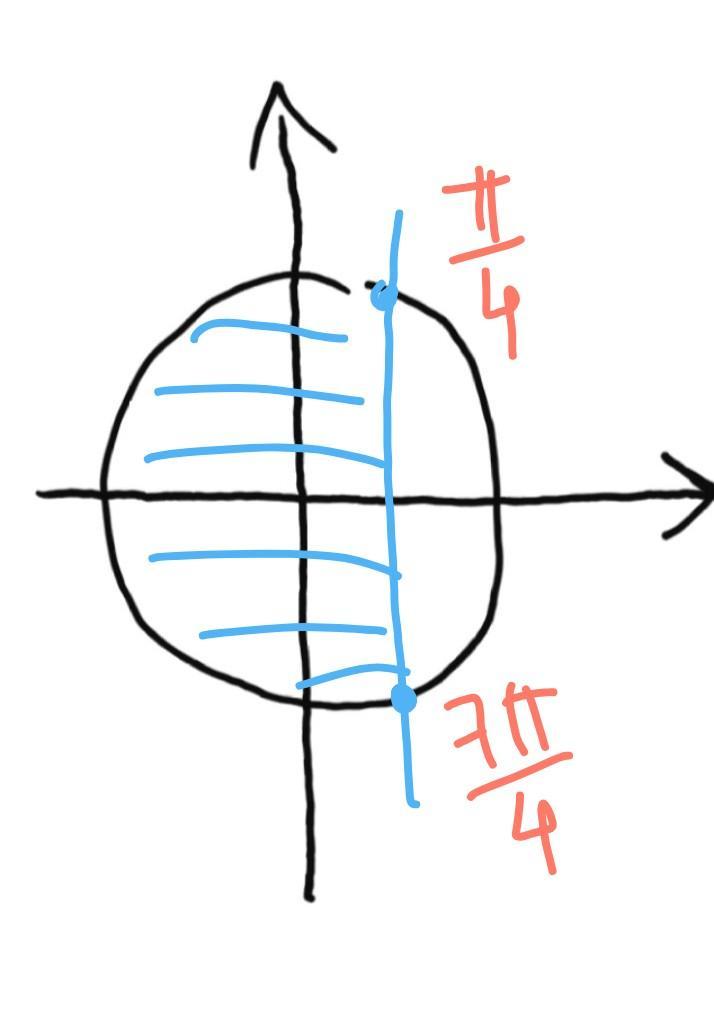
д)
рисунок2
везде n принадлежит Z.
Приложения:
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: moskal2281
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: мудрец331
Предмет: Алгебра,
автор: JulliaHelp
Предмет: Русский язык,
автор: Мадина1в