Question

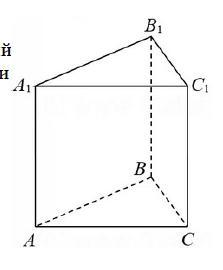
Основанием прямой треугольной призмы служит прямоугольный
треугольник с катетом ВС=5 см и гипотенузой АС=13 см. Периметр грани
СС1В1В составляет 40 см. Найдите площадь боковой поверхности призмы.

Answer 1

Ответ:

450см²

Объяснение:

∆АВС- прямоугольный треугольник

По теореме Пифагора

АВ=√(АС²-ВС²)=√(13²-5²)=√(169-25)=

=√144=12см.

Р(СС1В1В)=2(ВС+СС1)

СС1=Р(СС1В1В)/2-ВС=40/2-5=20-5=15см

Sбок=Росн*СС1

Росн=АВ+ВС+АС=5+13+12=30см

Sбок=30*15=450см²

Answer 2

Ответ:

Объяснение:

Катет в основании АС=√(13^2-5^2)

АС=√(13-5)(13+5)=√8*18=4*3=12

Р(СС1В1В)=2(ВС+СС1)

2(5+СС1)=40

СС1=15

Sбок=Росн*СС1

Sбок=(13+5+12)*15=30*15=450