Предмет: Математика,
автор: dima20063004
ДАЮ 15 БАЛЛОВ Наименьшее значение функции y=x2−6x+a равно 1. Найдите ординату её точки пересечения с осью ординат.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y=x²−6x+a это парабола ветвями вверх
у нас есть минимальное значение функции у = 1
мы пойдем путем, обратным пути поиска экстремума функции.
найдем, в какой точке достигается минимум (а минимум достигается в точке х0, где производная функции равна 0)
y'(x) = 2x -6 2x-6 = 0 ⇒ x = 3
таким образом вершина нашей параболы (ее минимум) достигается в точке (3; 1), т.е. парабола проходит через эту точку. отсюда найдем а
у(3) = 3²−6*3+a = 1 ⇒ а = 10
таким образом мы восстановили уравнение
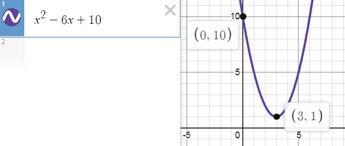
у = x²−6x+10
тогда точка пересечения с осью ординат (0; 10) , а ее ордината
у = 10
Приложения:
dima20063004:
спасибо огромное))
пожалуйста -))
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: БСП1
Предмет: Русский язык,
автор: maximefimchenk
Предмет: Геометрия,
автор: Maxon2n
Предмет: Английский язык,
автор: alenama1