Предмет: Математика,
автор: xedodir136
вычислить объем тела образованного вращением фигуры ограниченной линиями вокруг оси ox. y=8+2x- , y=2x+4 , y=0, x=0
, y=2x+4 , y=0, x=0
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
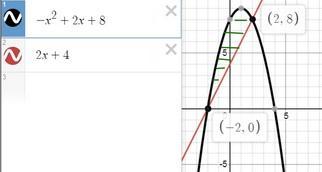
рисуеи графики, определяем фигуру, границы интегрирования
когда будем вертеть эту штуку вокруг оси ох, получим такую чашу с конусом внутри и выпуклыми боками.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: raisatmagomedo1
Предмет: Русский язык,
автор: Антон22308
Предмет: Английский язык,
автор: sarinet1631
Предмет: Математика,
автор: XMango