Question

Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 78 см, а одна из сторон
равна 18 см. Найдите две
другие стороны треугольника.​

Answer 1

Ответ:

30 и 30, 18 и 42

Объяснение:

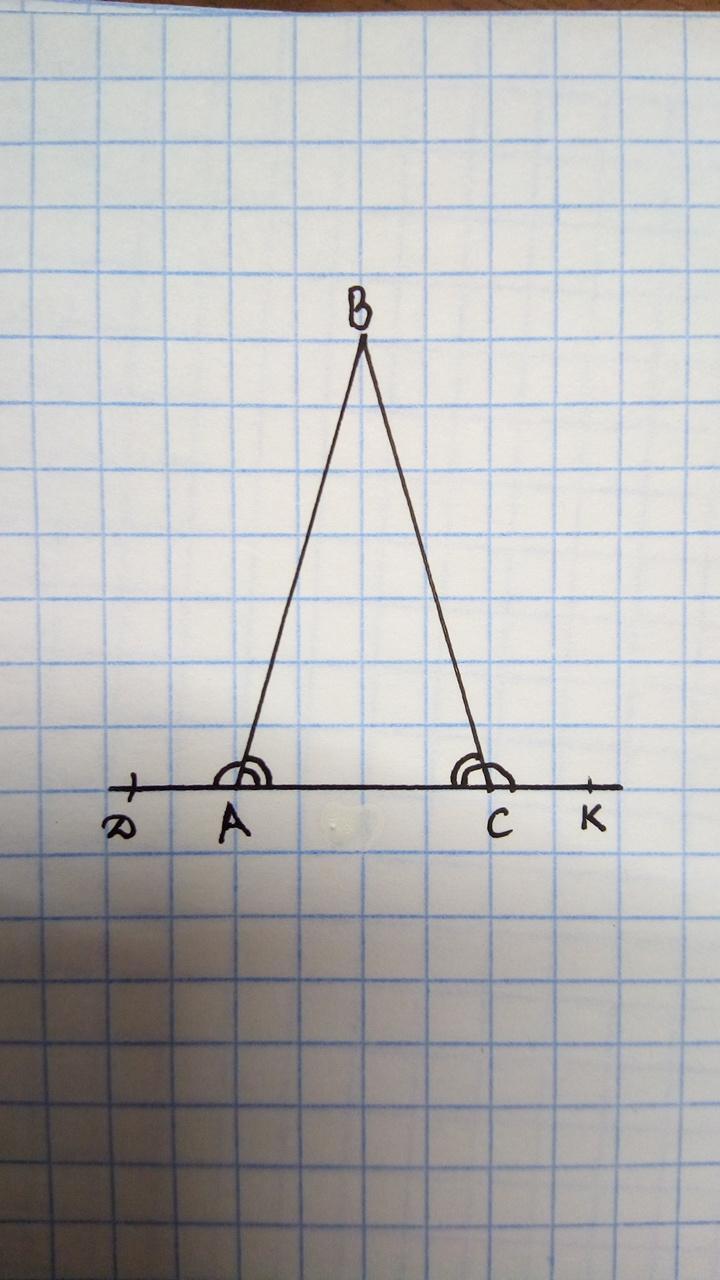
Возьмём произвольный треугольник АВС. Углы ВАD и ВСК внешние, угол ВАD=углу ВСК по условию. Угол ВАС=180°-угол ВАD (смежные) и угол ВСА=180°-угол ВСК (смежные). Угол ВАD=углу ВСК=> угол ВАС =180°-угол ВАD=180°-угол ВСК= углу ВСА. Угол ВАС = углу ВСА=> треугольник АВС - равнобедренный и по свойству АВ=ВС.

1. Пусть АВ=ВС=х, тогда Р=АВ+ВС+АС= х+х+18 =2х+18=78, 2х=78-18=60, х=30=> АВ=ВС=30.

Ответ: 30 и 30

2. Пусть АВ=18, тогда АВ=ВС=18. Р=АВ+ВС+АС=18+18+АС=36+АС=78, АС = 78-36=42.

Ответ: 18 и 42.

Р.с. получилось 2 пункта, т.к. в условии не сказано какая из сторон равна 18, поэтому мы рассматриваем 2 варианта, когда АС=18 и когда АВ=ВС=18.