Предмет: Геометрия,
автор: greatboy2511
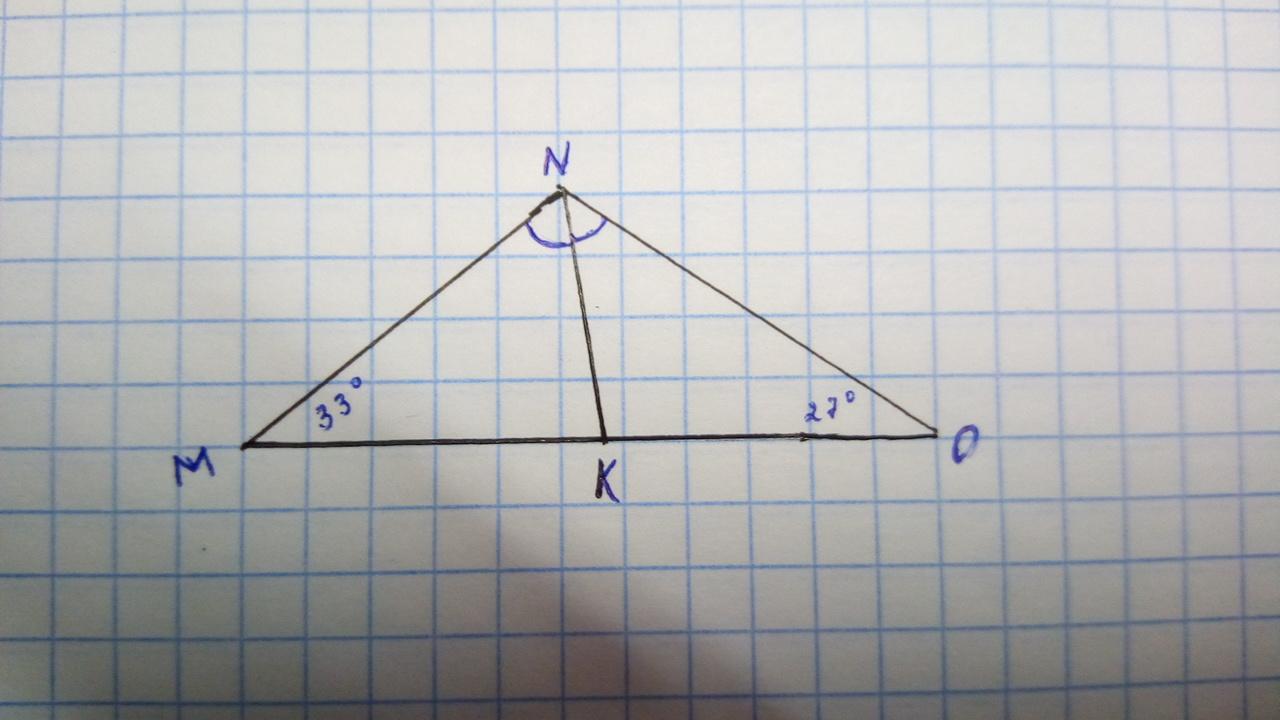
Дан произвольный треугольник MNO, в котором проведена биссектриса одного из углов. Известно, что два угла равны 33° и 27°, и проведённая биссектриса не имеет общих точек с вершинами этих углов. Вычисли, какой угол получился между этой биссектрисой и стороной угла, из которого она проведена.
ХЕЕЛП ПЛЗ
Ответы
Автор ответа:
2
Ответ:
60°
Объяснение:
Пусть NK - биссектриса угла N, тогда угол М равен 33°, а угол О равен 27°. Сумма всех углов треугольника равна 180° => угол М+угол N+ угол О=180°, 33°+ угол N+27°=180°, угол N=180°-33°-27°=180°-60°= 120°. NK биссектриса => угол МNK равен углу KNO = 120°:2=60°.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: карина0051
Предмет: Қазақ тiлi,
автор: kluchunikovvla
Предмет: Русский язык,
автор: rasulabbasov
Предмет: Литература,
автор: Аноним
Предмет: Русский язык,
автор: yliana24