Предмет: Алгебра,
автор: мрррррррррррррррр
Объясните пожалуйста, как делать? Желательно пошагово, спасибо
Приложения:
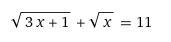
Ответы
Автор ответа:
1
Ответ:
Решение на фото
ответ 225 не является решением, записывать его не нужно
Приложения:

artem321321:
блин, там не все видно
как ещё раз отправить здесь
Вот, теперь кажется нормально
А откуда перед "x" берётся "22" и потом ещё "+x"?
А, мы в квадрат возводим. Всёё, дошло. Спасибо)
Все получилось?
Да
Автор ответа:
1
Ответ:
Объяснение:
Решим уравнение с помощью теоремы Виета:
Корень x₂ не подходит. Остаётся корень x₁ .
Похожие вопросы
Предмет: Русский язык,
автор: 2022ник
Предмет: Русский язык,
автор: узнавайка2004
Предмет: Русский язык,
автор: lizmaslowa2014
Предмет: Химия,
автор: Vanilla125