Предмет: Математика,
автор: danyaaaaaaa7
Решите пожалуйста. Ничо не знаю
Приложения:
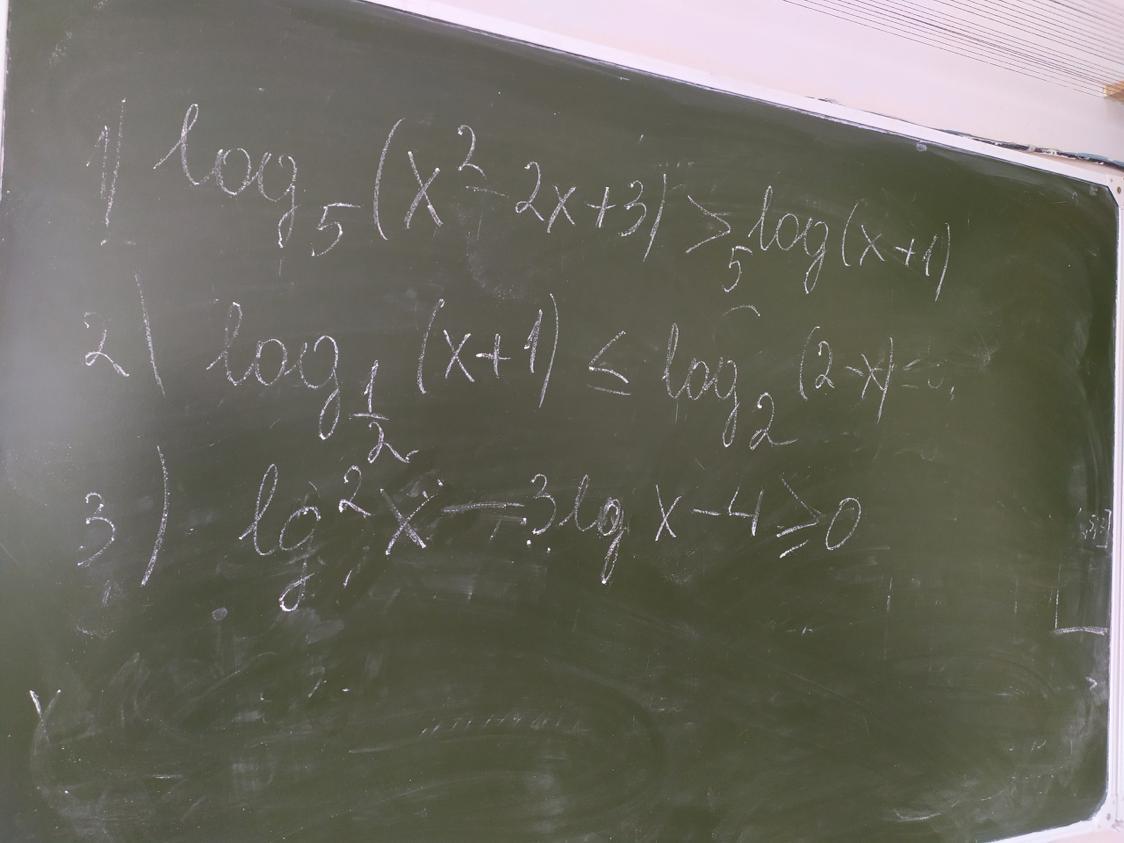
Ответы
Автор ответа:
1
Ответ:
1.
ОДЗ:
С ОДЗ пересекаем
Ответ:
2.
ОДЗ:
Пересекаем с ОДЗ
Ответ:
3.
Пересекаем с ОДЗ, Ответ:
danyaaaaaaa7:
Спасибо большое❤️
МНЕ ПОМОГИТЕ УМОЛЯЮ ПОЖАЛУЙСТА
Похожие вопросы
Предмет: Українська література,
автор: VeronikaKungurova
Предмет: Русский язык,
автор: FRED123456
Предмет: Русский язык,
автор: Colhze
Предмет: Алгебра,
автор: bobkovaleksand1
Предмет: История,
автор: Banan793