Предмет: Математика,
автор: aagruk5678
помогите решить,дам 100 баллов кто решит этот вариант
Приложения:
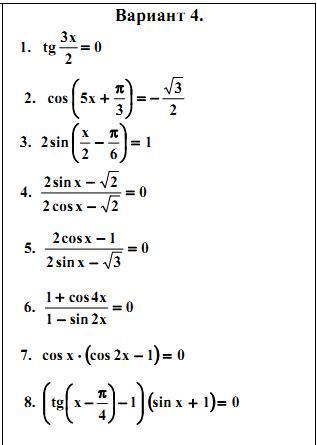
Ответы
Автор ответа:
2
Ответ:
1.
2.
3.
4.
Оба уравнения имеют одинаковые корни, но знаменатель не должен быть равен 0.
Ответ: корней нет
5.
Один из корней не подходит
Ответ:
6.
два корня не подходят
Ответ:
7.
Ответ:
8.
везде n принадлежит Z.
aagruk5678:
спасибо !!
не вижу вопроса
Похожие вопросы
Предмет: Русский язык,
автор: умник297
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: pnasta
Предмет: Математика,
автор: ксюша1794