срочно 45 баллов
16 и 20 задачи
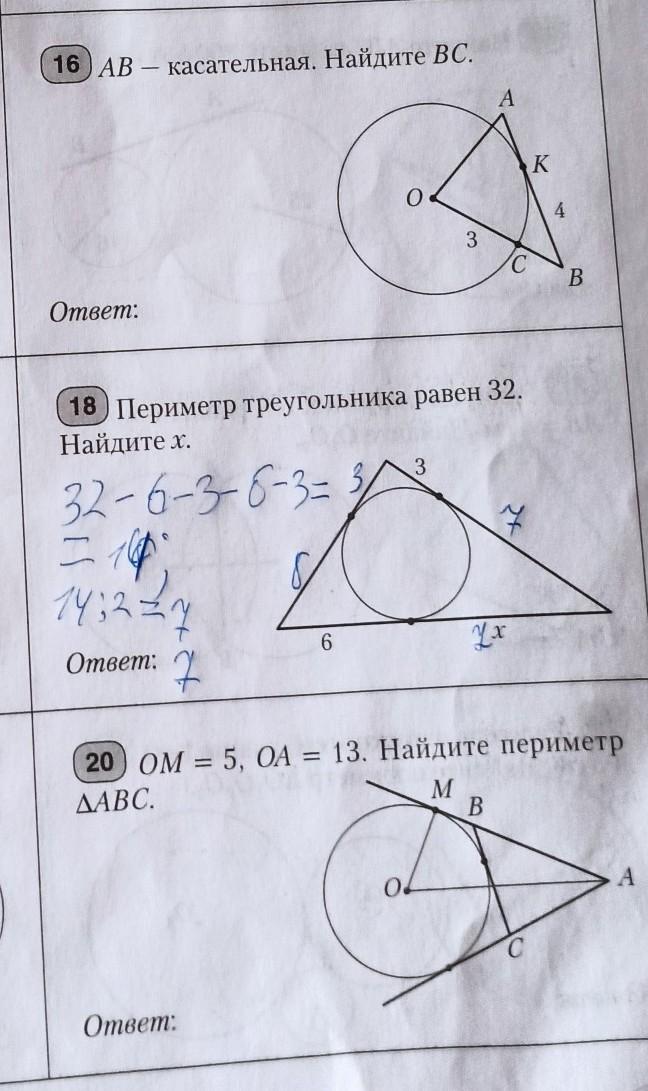
Ответы
Ответ:
16) 2
20) 24
Объяснение:
16) Если продолжить луч BO до вторичного пересечения с окружностью (назовём в точке H), мы получим секущую BH;
BK - отрезок касательной, BH - секущая; тогда найдём отрезок секущей BC по формуле:
Так как задача в нахождении отрезка - BC не может быть отрицательной величиной; ответ BC1 = 2
18) Обозначим точку касания с прямой BC - H, с прямой AC - K:
MB = BH (отрезки касательных)
CH = CK (так же отрезки касательных)
Рассмотрим треугольник AMO:
AMO - прямоугольный; тогда:
Периметр ABC = AB + AC + BC, при чём BC = BH + CH
Pabc = AB + AC + BH + CH
При чём AB = AM - MB ; AC = AK - CK
Подставим ещё раз:
Pabc = AM - MB + AK - CK + BH + CH
Так как MB = BH, CH = CK:
Pabc = AM - BH + AK - CH + BH + CH = AM + AK
AM = AK (отрезки касательных)
Pabc = 2AM = 2 * 12 = 24