Question

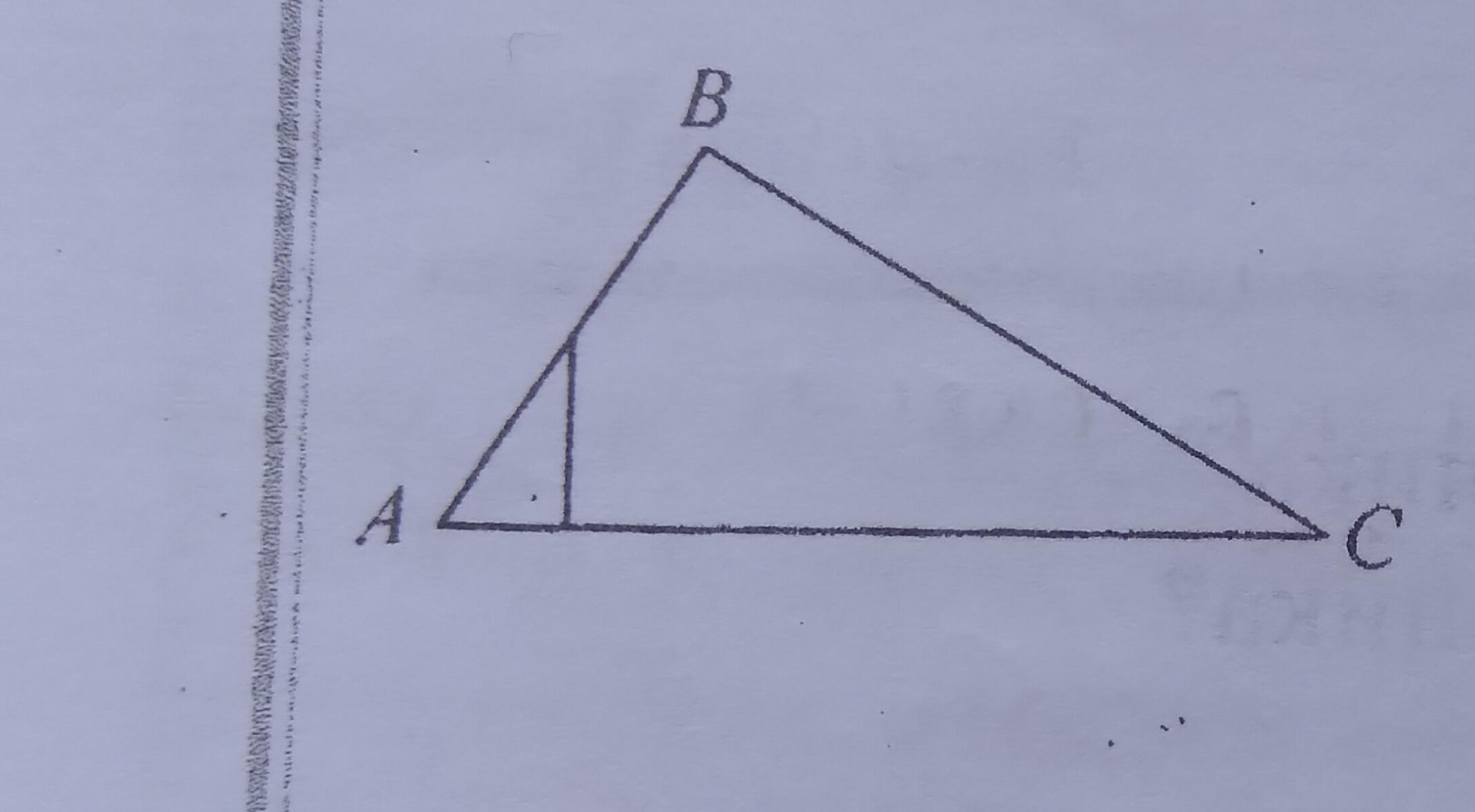
1.Из середины стороны АВ треугольника АВС опущены перпендикуляр длиной 4 см на сторону АС. Найдите длину высоты в треугольнике проведённую из вершины В.
2. В прямоугольной треугольнике длины перпендикуляров, опущенных из середины гипотенузы на катеты, соответственно равны 6см и 4,5 см. Найдите гипотезу треугольника.

Answer 1

Ответ:

1) 8см 2)15см

Пошаговое объяснение:

1)высота BH

т.к. треугольники подобны и точка лежит посередине, то коээфициент подобия=2

4*2=8см

2)

т.к. перпендикуляры проведены из середины гипотенузы, то по теореме фалеса, перпендикуряры делят катеты пополам, значит длина одного катета 4,5*2=9, а длина второго - 6*2=12

по теореме Пифагора

9²+12²=с²

81+144=с²

с²=225

с=15