Предмет: Алгебра,
автор: litvincevam025
Постройте график функции
y=x|x| + |x| – 5х
Определите, при каких значениях m прямая у=m имеет с графиком ровно две общие
точки. ПОМОГИТЕ ПОЖАЛУЙСТА
Ответы
Автор ответа:
1
Объяснение:
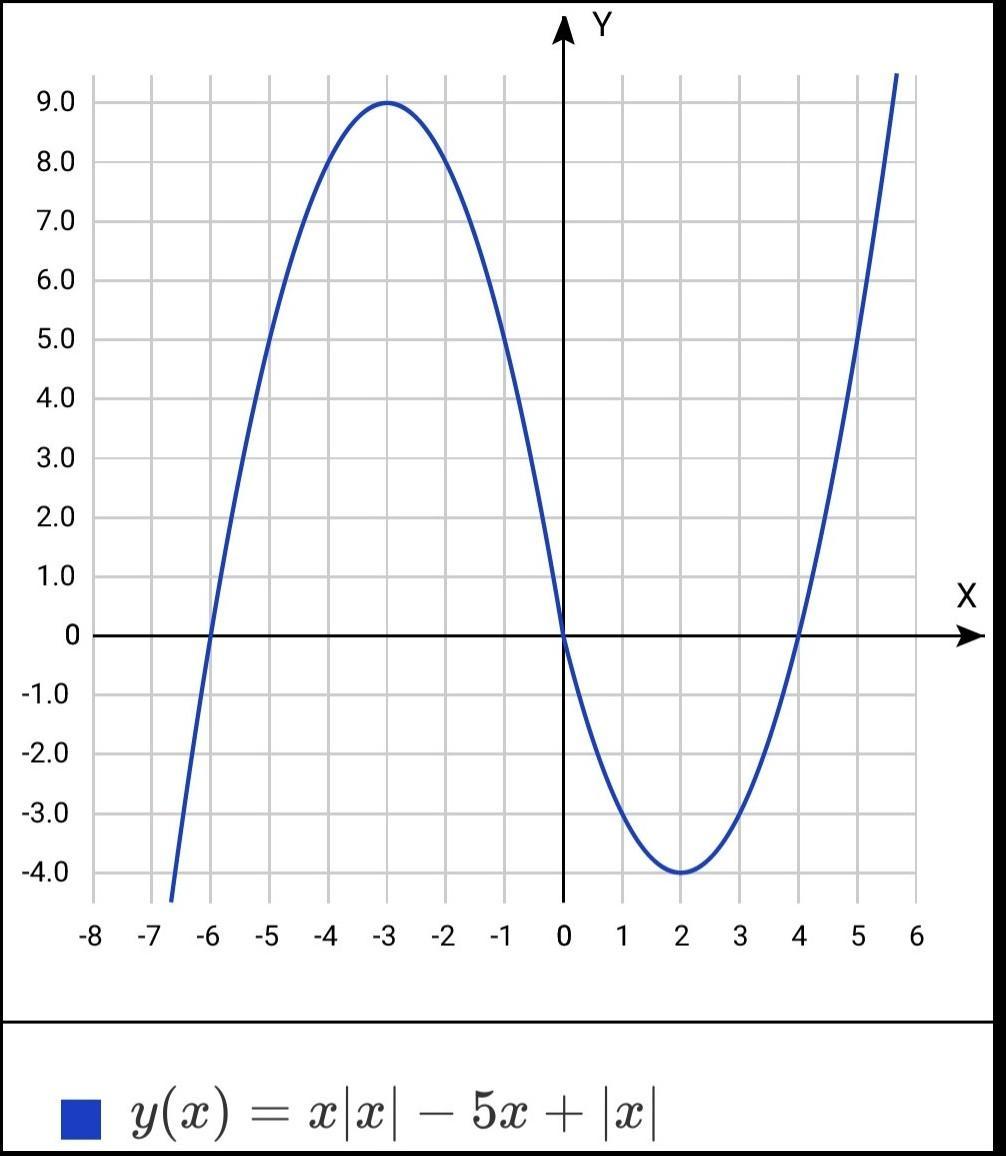
График ф-ии см. на рис.
Как видно из графика, только 2 общих точки с графиком прямой
у = m
имеются в точках экстремума ф-ии.
Найдем их:
Найдем значение у в точках экстремума
Соответственно, искомые значения m:
m = 9
m = -4
Приложения:
litvincevam025:
спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Українська мова,
автор: mila2017
Предмет: Русский язык,
автор: Новичок456
Предмет: Українська мова,
автор: Кондратьева2004
Предмет: История,
автор: SashaVolsjaia