Предмет: Геометрия,
автор: zhasmin256
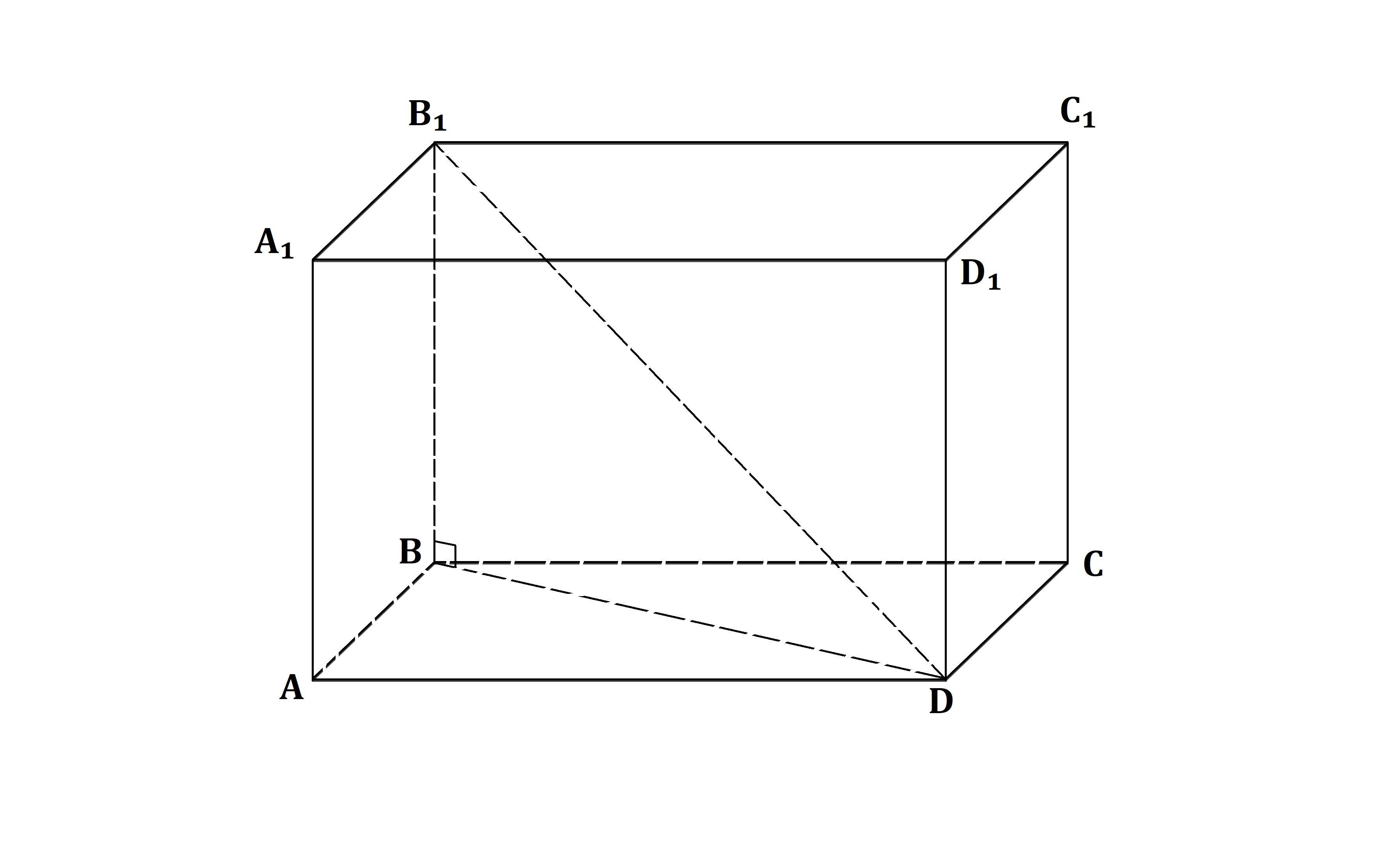
Найдите площадь боковой поверхности и объем прямоугольного параллелепипеда ABCDA1B1C1D1
если B1D = 20 см, AD = 8 см, угол B1DB = 60°.
Ответы
Автор ответа:
2
Ответ: площадь боковой поверхности прямоугольного параллелепипеда равна 280√3 см²; объём прямоугольного параллелепипеда равен 480√3 см³
Объяснение:
ΔB₁BD - прямоугольный, так как ABCDA₁B₁CD₁ - прямоугольный параллелепипед.
- Сумма острых углов в прямоугольном треугольнике равна 90°.
⇒ ∠BB₁D = 90° - ∠B₁DB = 90° - 60° = 30°
- Если в прямоугольном треугольнике острый угол равен 30°, то противолежащий катет равен половине гипотенузы.
⇒ BD = B₁D : 2 = 20 : 2 = 10 см
- Если в прямоугольном треугольнике острый угол равен 60°, то противолежащий катет равен произведению меньшего катета на √3.
⇒ BB₁ = BD · √3 = 10 · √ 3 = 10√3 см
или по другому:
Найдём BB₁ по теореме Пифагора:
см
- Основание прямоугольного параллелепипеда - прямоугольник.
То есть ΔABD - прямоугольный
По теореме Пифагора найдём AB:
см
- S бок. поверхн. = P основ. · BB₁ (произведение периметра основания параллелепипеда на высоту параллелепипеда)
P основ. - периметр прямоугольника ABCD
⇒ P основ. = (AB + AD) · 2 = (6 + 8) · 2 = 14 · 2 = 28 см
⇒ S бок. поверхн. = 28 · 10√3 = 280√3 см²
- V = AB · AD · BB₁ (произведение всех 3 измерений параллелепипеда - длины, ширины и высоты)
V = 6 · 8 · 10√3 = 48 · 10√3 = 480√3 см³
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: khromova1
Предмет: Русский язык,
автор: ольгаz
Предмет: Русский язык,
автор: lazzatau
Предмет: Математика,
автор: ан04на
Предмет: Химия,
автор: bmlove01