Предмет: Математика,
автор: mikedonaldor
Найдите производную.
Приложения:
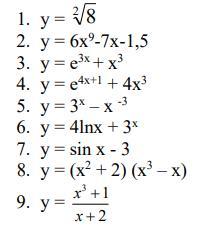
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Похожие вопросы
Предмет: Русский язык,
автор: STUDENTKA124
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Darya1116
Предмет: Русский язык,
автор: Инструмент
Предмет: Физика,
автор: PisarenkoEV1