Предмет: Алгебра,
автор: Аноним
правильно ли я решила? если нет исправьте пж
Приложения:

Ответы
Автор ответа:
0
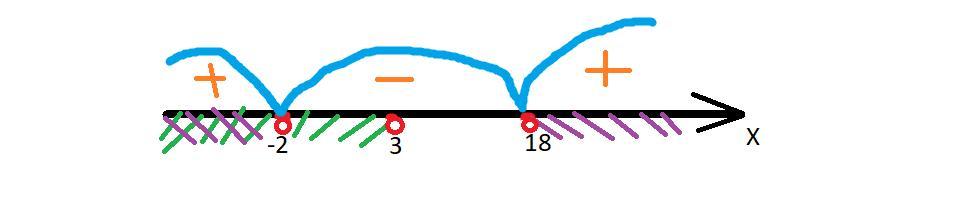
Ответ:
x є (-∞;-2)
Объяснение:
6 - 2x > |x + 12| ⇔
⇒ x є (-∞;-2)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: wwwyalbakova19
Предмет: Окружающий мир,
автор: lions54
Предмет: Русский язык,
автор: kallayarova
Предмет: Другие предметы,
автор: kedrovskij135p6eq0d
Предмет: Английский язык,
автор: Blaguk