Предмет: Геометрия,
автор: jjjjjku
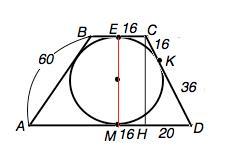
Одна из боковых сторон трапеции равна 60 см, а другая точкой касания окружности, вписанной в данную трапецию, делится на отрезки 16 и 36 см. Вычислите плошадь трапеции.
Ответы
Автор ответа:
3
Ответ: 2688 см²
Объяснение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
Для трапеции АВСD, в которую вписана окружность, BC+AD=AB+CD=60+16+36=112 см.
Стороны трапеции - касательные к вписанной окружности. Обозначим точки касания на ВС– Е, на СD - К, на AD-М. По свойству равенства отрезков касательных, проведенных из одной точки, СЕ=СК=16, DK=DM=36.
Соединим точки касания на основаниях отрезком ЕМ. Опустим высоту СН. МН=ЕС=16
DH=DM-CE=36-16=20.
По т.Пифагора СН=√(CD²-DH²)=√(52²-20²)=48 (см)
Площадь трапеции равна произведению полусуммы оснований на высоту.
S(ABCD)=0,5(BC+AD)•CH=0,5•112•48=2688 см².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Анна831201
Предмет: Русский язык,
автор: catcat9890
Предмет: Другие предметы,
автор: Lesya010101
Предмет: Математика,
автор: Vinogradik166