Предмет: Алгебра,
автор: Dv1ishnik
Найти производные функции
Заранее благодарю
Приложения:
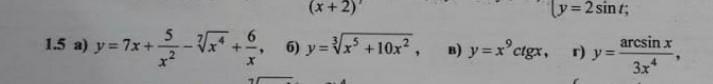
Ответы
Автор ответа:
1
Ответ:
a
б
в
г
Похожие вопросы
Предмет: Немецкий язык,
автор: Аноним
Предмет: Русский язык,
автор: sumtimofey20088
Предмет: Українська мова,
автор: keks64011
Предмет: Алгебра,
автор: AliceYu
Предмет: История,
автор: kyryl0s