Предмет: Математика,
автор: MolkyWay
Спасите!!! СРОЧНО!!!!
Приложения:
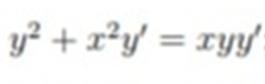
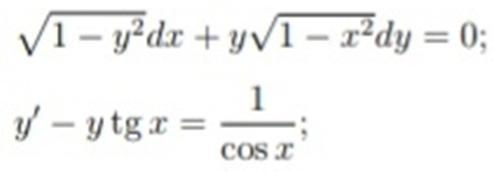
Ответы
Автор ответа:
1
Ответ:
MolkyWay:
Спасибо вам)
Похожие вопросы
Предмет: Русский язык,
автор: настя685
Предмет: Другие предметы,
автор: куке2
Предмет: Қазақ тiлi,
автор: Amirka1111
Предмет: Геометрия,
автор: Htyyy29