Question

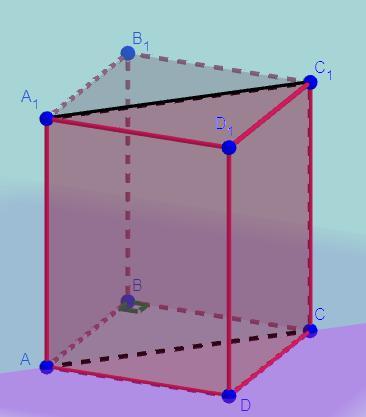
у правильній чотирикутній призмі площа основи дорівнює 144 см² , а висота 10 см. знайдіть площу діагонального перерізу.​

Answer 1

Ответ:

$S_{ABCD} = 120\sqrt{2}$ см²

Объяснение:

Дано: $ABCDA_{1}B_{1}C_{1}D_{1}$ - правильна чотирикутна призма,

$S_{ABCD} =$ 144 см², $AA_{1} =$ 10 см

Знайти: $S_{p} \ - \ ?$

Розв'язання:

За означенням правильна призма - це пряма призма в основі якої лежить правильний многокутник, отже так як за умовою  $ABCDA_{1}B_{1}C_{1}D_{1}$ - правильна чотирикутна призма, то так як в основі лежить правильний чотирикутник, то ABCD - квадрат.

За властивістю правильної призми її висотою є бічне ребро.

За формулою площі квадрата:

$S_{ABCD} = AB^{2} \Longrightarrow AB = \sqrt{S_{ABCD}} = \sqrt{144} = 12$ см.

За властивістю квадрата усі його кути дорівнють 90° і усі сторони рівні, отже AB = BC = 12 см, кут ∠ABC = 90°.

Розглянемо трикутник ΔABC. Трикутник ΔABC - прямокутний, так кут ∠ABC = 90°, отже за теоремою Піфагора:

$AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{12^{2} + 12^{2}} = \sqrt{144 + 144} = \sqrt{288} = 12\sqrt{2}$ см.

За властивістю правильної призми ($ABCDA_{1}B_{1}C_{1}D_{1}$) її діагональним перерізом є прямокутник сторонами якого є діагональ, що лежить в основі (квадрат) і бічне ребро призми, тоді за формулою площі прямокутника:

$S_{ABCD} = AA_{1} \cdot AC = 12\sqrt{2} \cdot 10 = 120\sqrt{2}$ см².