Question

Из точки над плоскостью проведены две наклонные, образующие с плоскостью углы 45° и 30°, а между собой угол 90°. Самая длинная наклонная - 8 см. Найдите расстояние между концами наклонных.
Только очень прошу поподробнее! Заранее спасибо!

Answer 1

Відповідь:

Пояснення:

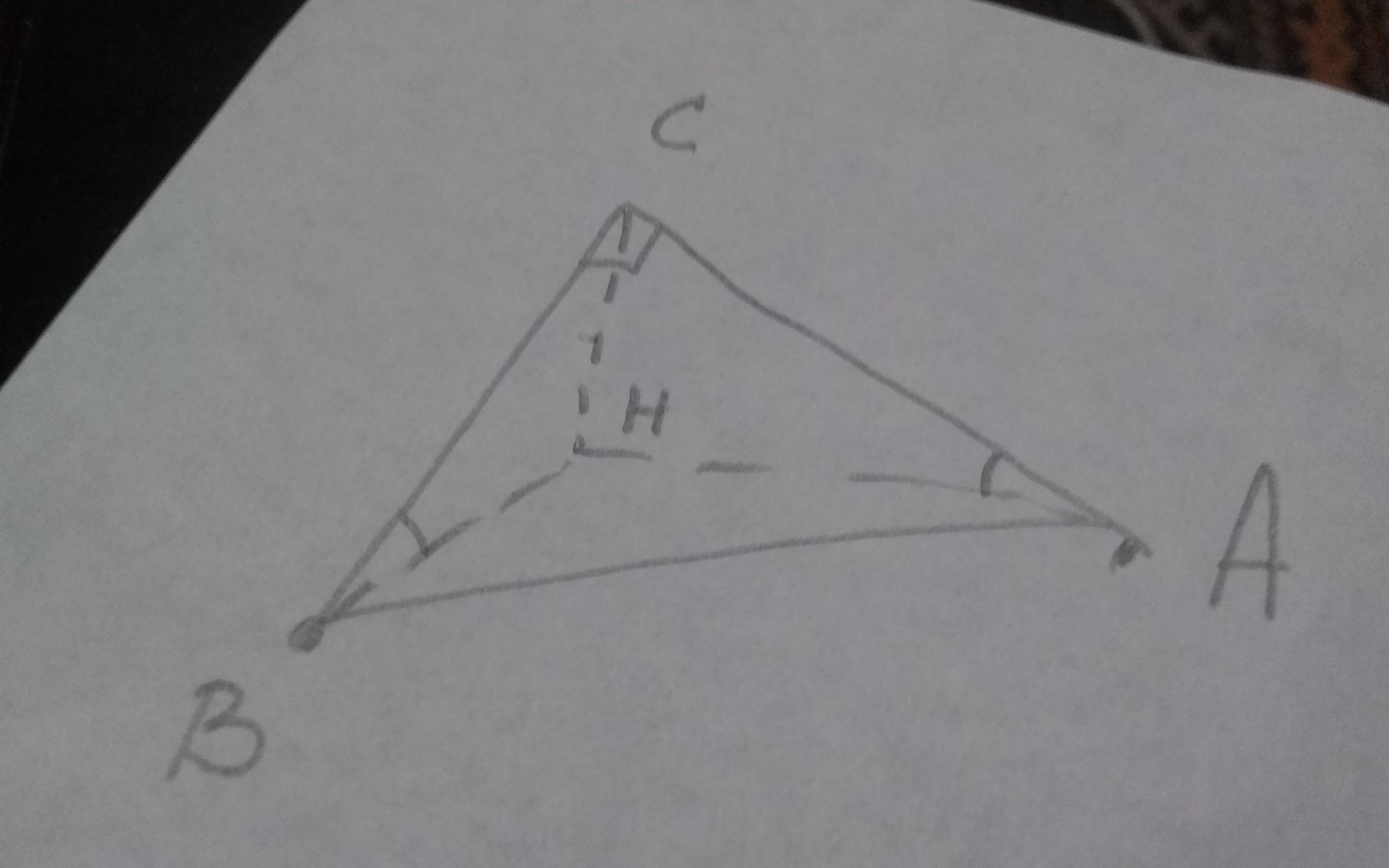
Пусть с точки С опустили две наклонние на плоскость, в пересечении получили точки А и В

В результате имеем △АВС, где /_С=90°

Опустим перпендикуляр с точки С на плоскость, получим точку Н

Известно, что /_САН=45° и /_СВН=30°, СВ=8

Тогда из △СНВ /_Н=90°, /_В=30° и СВ=8 имеем

СН=4, как катет против угла 30°

Из △СНА, где /_Н=90° и /_А=45° следует, что и /_НСА=45° → △СНА равнобедренний → СН=НА=4

По теореме Пифагора СА=4√2

Из △АВС: /_С=90°, из условия, СВ=8, СА=4√2

За теоремою Пифагора

ВА^2=СВ^2+СА^2=64+32=96

ВА=4√6