Предмет: Геометрия,
автор: vv281578
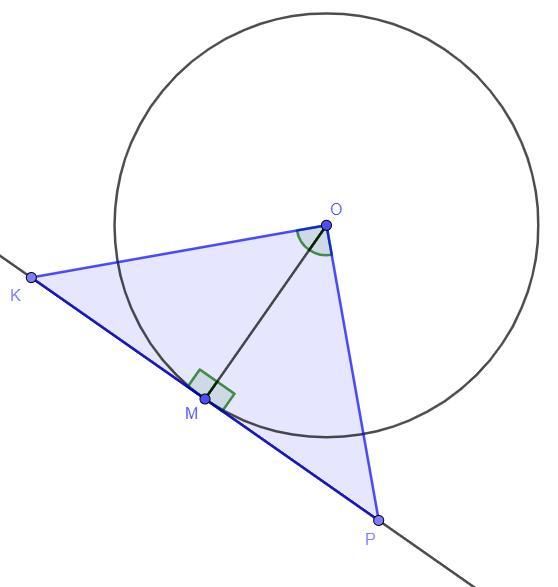
прямая касается окружности с центром о в точке м на касательной по разные стороны от точки м отметили точки к и п какие что уголMOK=MOP.Найдите угол окм ,если угол опм=48
Ответы
Автор ответа:
9
Ответ:
∠OKM = 48°
Объяснение:
Дано: KP - касательная, O - центр окружности, ∠MOK = ∠MOP,
∠OPM = 48°
Найти: ∠OKM - ?
Решение:
Так как по условию KP - касательная, то угол ∠KMO = ∠PMO = 90°.
Треугольник ΔMOK = ΔMOP по двум углам, так как угол по условию угол ∠MOK = ∠MOP, а угол ∠KMO = ∠PMO = 90° и сторона
MO - общая.
Так как треугольник ΔMOK = ΔMOP, то соответствующие элементы равны, тогда угол ∠OKM = ∠OPM = 48°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ksyudanilova
Предмет: Русский язык,
автор: mmmnnnn
Предмет: Русский язык,
автор: влад222221
Предмет: ОБЖ,
автор: stavr2356