Предмет: Алгебра,
автор: Anseaymi
Решите, пожалуйста, 15 номер
Приложения:
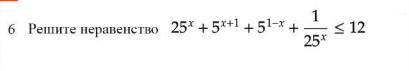
Ответы
Автор ответа:
1
Ответ:
Приведён в фото вместе с решением
Объяснение:
Нетипичный вид работы с двойной заменой + отсекания корня до единственного значения
Приложения:
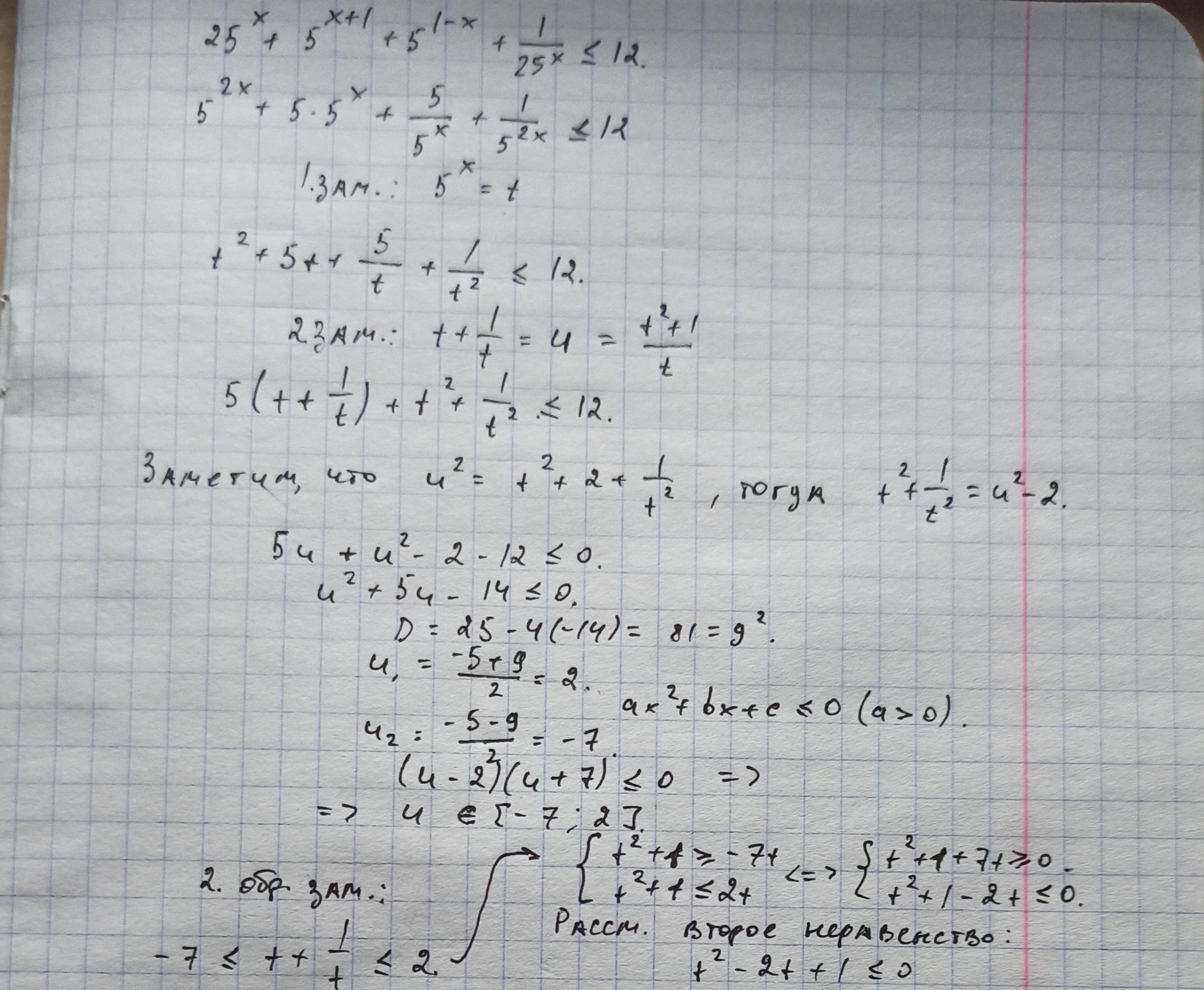

Автор ответа:
2
25ˣ+5ˣ⁺¹+5¹⁻ˣ+1/25ˣ ≤12
(5ˣ)²+5*5ˣ+5/5ˣ+1/25ˣ ≤ 12
(5²ˣ+1/5²ˣ)+5*(5ˣ+1/5ˣ) ≤ 12
Если (5ˣ+1/5ˣ) = t , то
t²= (5ˣ+1/5ˣ)² = 5²ˣ+2*5ˣ*1/5ˣ+1/5²ˣ=5²ˣ+2+1/5²ˣ ;
Значит 5²ˣ+1/5²ˣ=t²-2
t²-2+5t ≤ 12
t²+5t-14 ≤ 0
1) Найдём нули
D=25+4*14=25+56=81
t1=(-5+9)/2=4/2=2
t2=(-5-9)/2=-14/2=-7
-7 ≤ t ≤ 2 , т.е -7 ≤ 5ˣ+1/5ˣ ≤ 2 ИЛИ:
Нер-во примет вид:
система: 5ˣ+1/5ˣ ≥ -7
5ˣ+1/5ˣ ≤ 2
х- любое
5ˣ=y > 0
(y^2-2y+1)/y ≤ 0
2) y ≠ 0
3) (y-1)²=0, y=1
4) y<0 , y=1 , т.е 5ˣ=1
х=0
Ответ: х=0
Приложения:
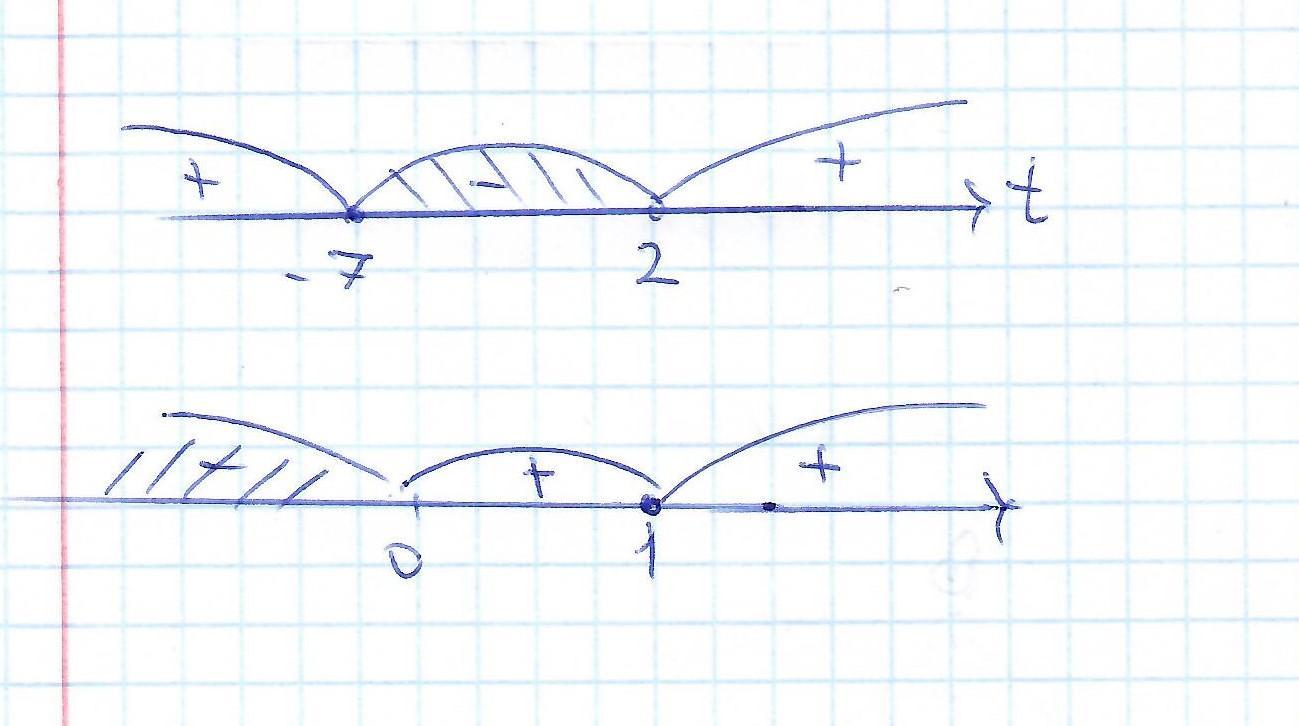
Похожие вопросы
Предмет: Окружающий мир,
автор: nikita4684786
Предмет: Українська мова,
автор: lockasi
Предмет: Русский язык,
автор: XIAO
Предмет: Геометрия,
автор: Darinks38
Предмет: Математика,
автор: NikSail