Question

Вычислить обьем тела, полученного вращением вокруг оси Ох фигур, ограниченных линиями: х=у^3;х=0;у=1.​

Answer 1

Ответ:

Пошаговое объяснение:

прежде всего перейдем от  х=у³  к более привычной записи

у = ∛х

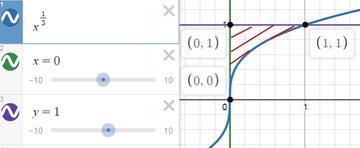
рисуем график, получаем фигуру

теперь можем искать объем, как разницу объемов тел, вращаемых вокруг оси ох,  V1 - образованного вращением квадрата 1х1  и V2 "чашей" образованной вращением у = ∛х

а можем сразу испорльзовать формулу

$\displaystyle V= \pi \int\limits^a_b {(y_1^2-y_2^2)} \, dx$

на графике "выше" лежит график функции у = 1 - он и будет у₁

тогда

$\displaystyle V= \pi \int\limits^1_0 {(1^2-(\sqrt[3]{x} )^2)} \, dx= \pi \bigg (x -\frac{3x^{5/3}}{5} \bigg ) \bigg |_0^1=\frac{2}{5} \pi$