Предмет: Алгебра,
автор: ToshikNSF
Найти угловой коэффициент касательной, проведенной к графику функции y=1/(x-2)^2 в точке с абсциссой x-1
Ответы
Автор ответа:
1
Ответ:
2 или 2/27 (непонятная запись в вопросе)
Объяснение:
Так как угловой коэффициент касательной равен значению производной в точке касания, то найдём производную:
Имеем x = 1 (или указано "-1", непонятно, но в таком случае для обоих решение):
Подставим X в уравнение производной:
Автор ответа:
0
Ответ: -2/27. См фото.
Объяснение:
Приложения:
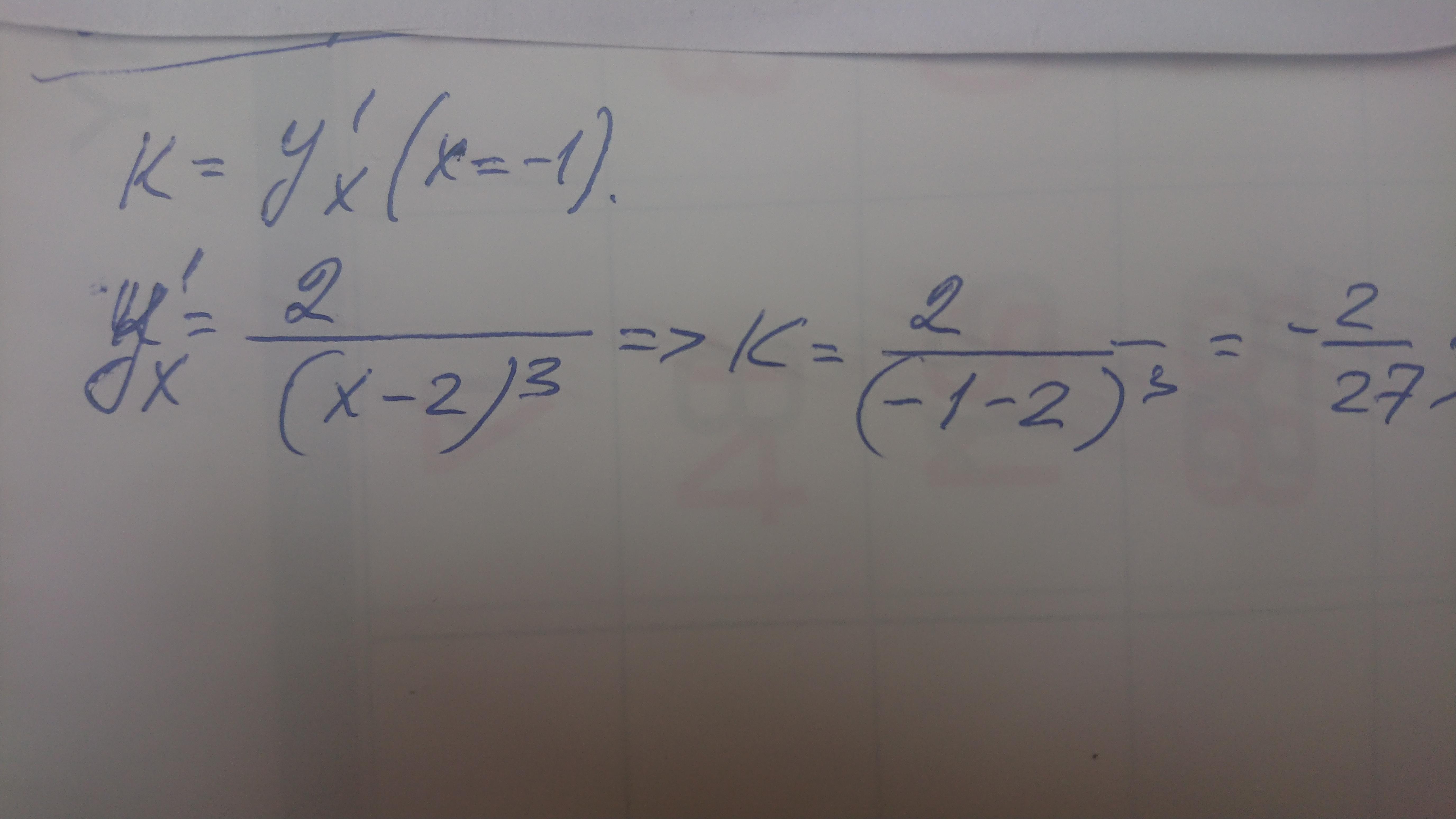
Zanmaru:
Забыли минус перед двойкой; множитель "-1" никуда не делся)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Зелим95
Предмет: Окружающий мир,
автор: MEMEKACHKA
Предмет: Химия,
автор: Просто100так