Предмет: Математика,
автор: elizavetacoj0
‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️
помогите решить эти два примера и объясните пожалуйста
‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️‼️
Приложения:
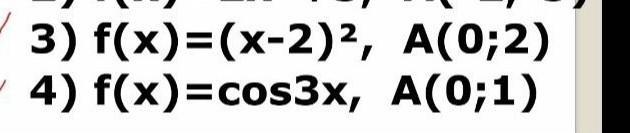
Miroslava227:
первообразная?
да
Ответы
Автор ответа:
1
Ответ:
3.
- общий вид
Подставляем координаты точки А
х = 0
у = 2
- ответ
4.
- общий вид
Подставляем координаты точки А
х = 0
у = 1
- ответ
вы не могли бы помочь мне с математикой?
Похожие вопросы
Предмет: Русский язык,
автор: elnara570esgmailcom2
Предмет: Русский язык,
автор: aminosin46
Предмет: Русский язык,
автор: Alsor599
Предмет: Литература,
автор: 1pikaPIKApika1
Предмет: Математика,
автор: Гаргомэль