Question

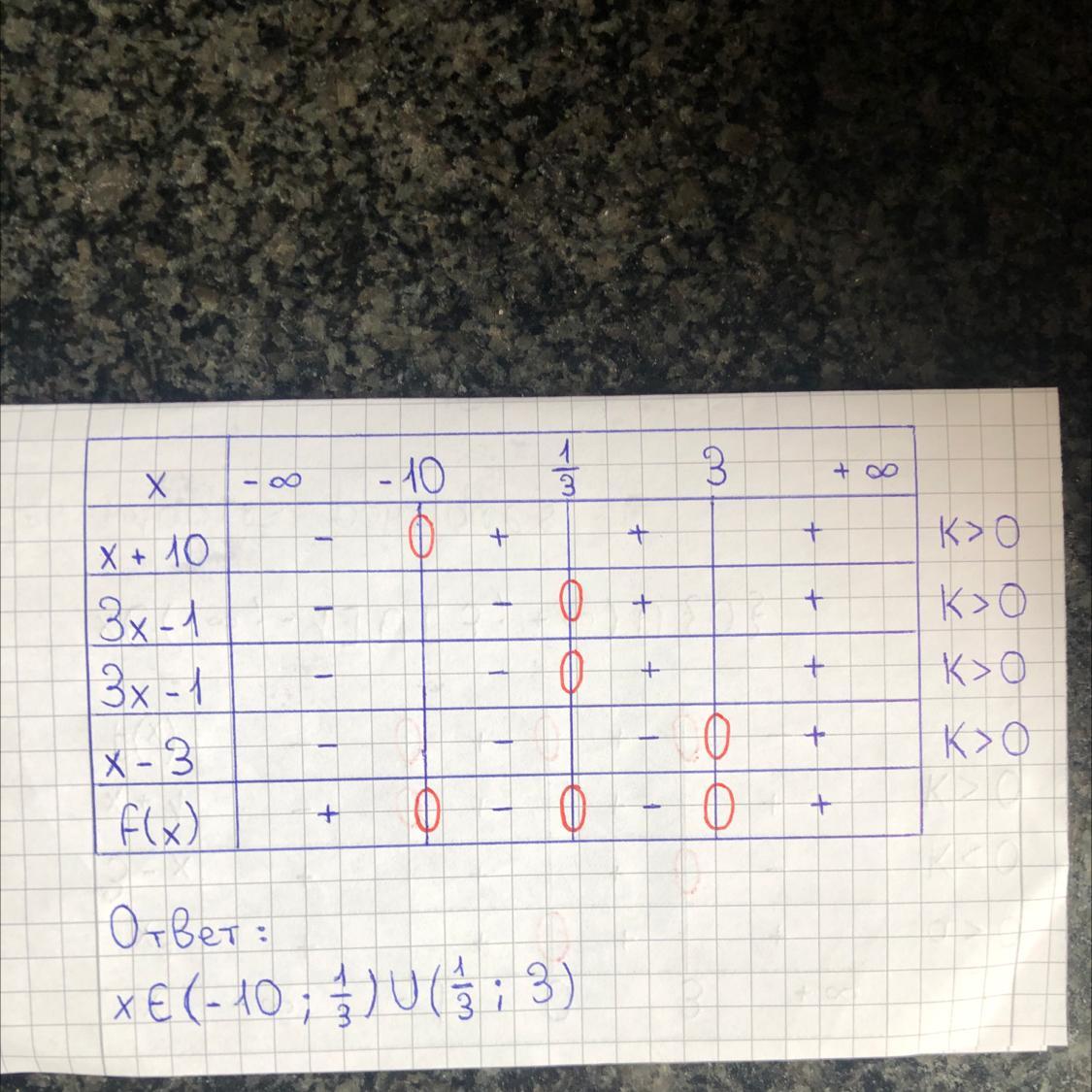
реши неравенство и найди произведение наибольшего и наименьшего целых решений (3x2 + 29x – 10)(3x2 – 10x + 3) < 0​

Answer 1

Ответ:

(3x² + 29x – 10)·(3x² – 10x + 3) < 0​

Приравняем неравенство к нулю:

(3x² + 29x – 10)·(3x² – 10x + 3) = 0​

произведение равно нулю, если хотя бы один из множителей равен нулю.

3x² + 29x-10=0 и 3x² – 10x + 3 = 0​.

1). 3x² + 29x-10=0

D = 29²-4·3·(-10) = 841+120 = 961 = 31²

$x_{1} = \frac{-29+\sqrt{961} }{2*3} = \frac{-29+31 }{6} = \frac{2}{6} = \frac{1}{3}$

$x_{1} = \frac{-29-\sqrt{961} }{2*3} = \frac{-29-31 }{6} = \frac{-60}{6} = -10$

2). 3x² – 10x + 3

D = -10²-4·3·3 = 100-36 = 64 = 8²

$x_{1} = \frac{10+\sqrt{64} }{2*3} = \frac{10+8}{6} = \frac{18}{6} = 3$

$x_{2} = \frac{10-\sqrt{64} }{2*3} = \frac{10-8}{6} = \frac{2}{6} = \frac{1}{3}$

Мы получили точки $-10; \frac{1}{3} ; 3$.

Нас интересуют точки которые меньше нуля

x∈(-∞;-10)∪(1/3; 3).

-10·3 = -30

Answer 2

Ответ: -18

Для начала приравняем данное выражение к нолю и попробуем найти корни. Для этого приравниваем каждый из множителей к нолю:

(1)

3x² + 29x - 10 = 0

D = 29² - 4×3×(-10) = 841 + 120 = 961 = 31²

x₁ = (-29 - 31) / 6 = -10

x₂ = (-29 + 31) / 6 = 1/3

3x² + 29x - 10 = (x + 10)(3x - 1)

(2)

3x² - 10x + 3 = 0

D = 10² - 4×3×3 = 100 - 36 = 64 = 8²

x₁ = (10 - 8) / 6 = 1/3

x₂ = (10 + 8) / 6 = 3

3x² - 10x + 3 = (3x - 1)(x - 3)

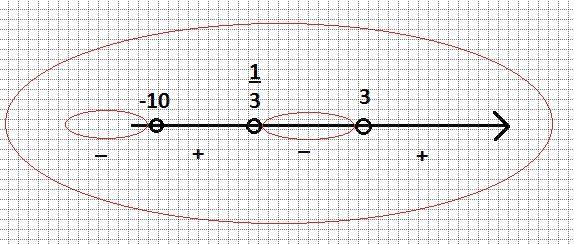
Теперь, находим интервалы x, при которых функция принимает отрицательные и положительные значения (см. прикреп. фото).

Теперь перемножаем наибольшее целое значение на наименьшее:

-9 × 2 = -18