Предмет: Математика,
автор: Lexuch
Для функції f на вказаному проміжку I знайдіть первісну F, графік
якої проходить через дану точку:
Приложения:
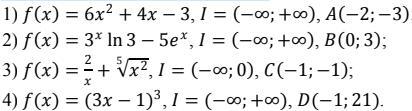
Ответы
Автор ответа:
0
Ответ:
1.
1)
- общий вид
В точке А:
2)
- общий вид
В точке В:
3)
- общий вид
В точке С:
4)
- общий вид
В точке D:
Похожие вопросы
Предмет: Русский язык,
автор: Jennifer08
Предмет: Английский язык,
автор: hellbent08
Предмет: Русский язык,
автор: Olya120404
Предмет: Русский язык,
автор: kitan75
Предмет: Русский язык,
автор: Evochcaзвезда