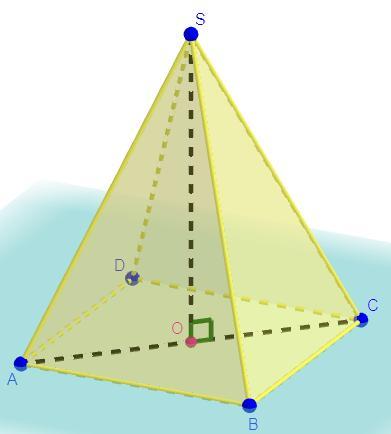
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO=76, AC=114. Найдите боковое ребро SD.
Ответы
Ответ:
см
Объяснение:
Дано: SACBD - правильная четырехугольная пирамида, O - центр основания, SO = 76, AC = 114
Найти: SD - ?
Решение:
По определению правильной пирамиды, в её основании лежит правильный четырехугольник, а так как по условию пирамида KABCD - четырехугольная, то ABCD - квадрат.
Так как по условию O - центр основания, по определению OS - высота пирамиды, то есть OS ⊥ ABC.
По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как OS ⊥ ABC и AC ⊂ ABC по построению, то SO ⊥ AC.
По свойствам правильной пирамиды все её боковые ребра равны, тогда SA = SB = SC = SD. Рассмотрим равнобедренный треугольник ΔSAC (SA = SC). По теореме высота проведенная к основания равнобедренного треугольника является медианой и высотой, тогда так как SO ⊥ AC, то так как SO - медиана, то AO = OC, следовательно AO = OC = AC : 2 = 114 : 2 = 57 см.
Так как SO ⊥ AC, то треугольник ΔSOC - прямоугольный, тогда по теореме Пифагора: см.
По свойствам правильной пирамиды все её боковые ребра равны, тогда SC = SD = 95 см.