СРОЧНО!!!
Длина внешней касательной двух окружностей в пять раз больше длины их внутренней касательной. Найдите расстояние между центрами этих окружностей, если их радиусы равны r и R.
Ответы
Ответ: √(R²+r²-13Rr/6)
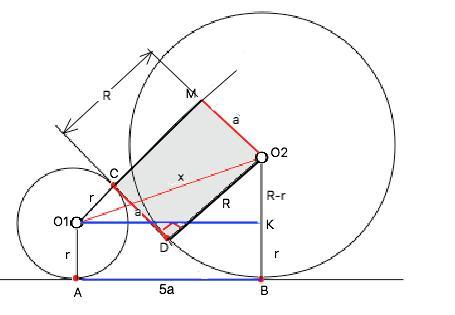
Объяснение: Обозначим центры окружностей О₁ и О₂.
Для удобства записи решения примем расстояние О₁О₂=х , СD=a. Тогда АВ=5CD=5a
Проведем из центров к точкам касания радиусы и проведем параллельно АВ прямую до пересечения с О₂В в точке К.
ABKO₁ - прямоугольник.=> KB=r
О₂К=R-r
О₁К=АВ=5а
Из О₂ к продолжению О₁С проведем перпендикуляр О₂М.
Четырехугольник СМО₂D- прямоугольник.
МО₂=СD=а
СМ=О₂D=R
MO₁=R+r
Из ∆ О₁MО₂ по т.Пифагора
а²=x²-(R+r)²
Из ∆ О₁КО₂ по т.Пифагора
(5а)²=х²-(R-r)²
Так как ОК=5а, подставим найденное выше значение а² во второе уравнение.
25a² =25•[x²-(R+r)²] ,
Приравняем найденные значения 25a².
25•[x²-(R+r)²]=х²-(R-r)²
После некоторых преобразований получим
24х²=24R²+24r²+52Rr, откуда
х=√(R²+r²-13Rr/6)= искомое расстояние между центрами окружностей