Предмет: Алгебра,
автор: sedovroma3
ПОМОГИТЕ ПОЖАЛУЙСТА, 2 ВАРИАНТ НАДО РЕШИТЬ
НЕ КОНТРОЛЬНАЯ А ДЗ НА ДОСКЕ НАПИСАЛИ, ПОЧЕМУ БАНЯТ ТО
Приложения:
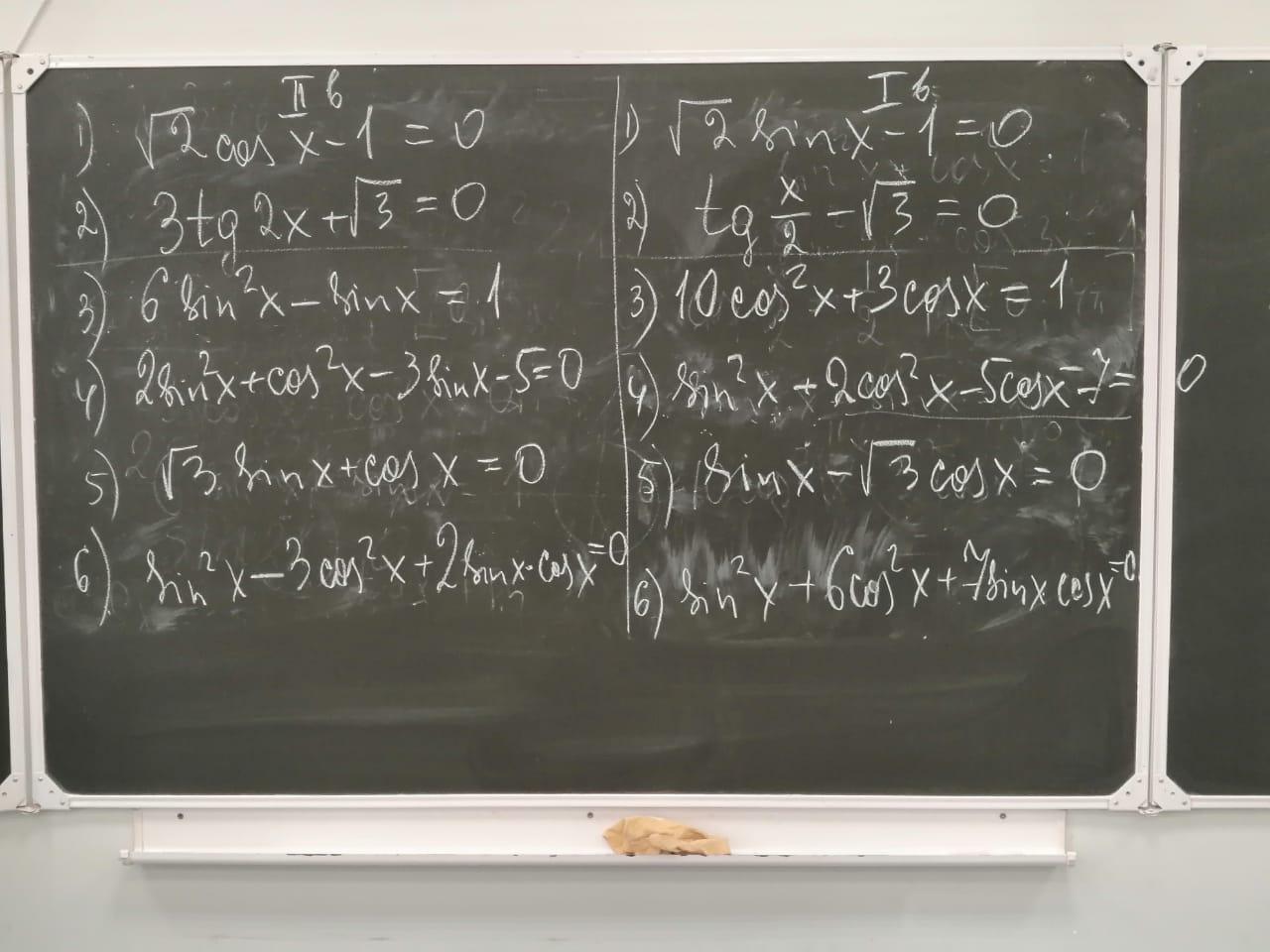
Ответы
Автор ответа:
1
Ответ:
1
2
3
4
5
6
везде n принадлежит Z.
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: GirlG100
Предмет: Английский язык,
автор: 180420041
Предмет: Математика,
автор: ник4974
Предмет: Психология,
автор: StrangeStud