Предмет: Алгебра,
автор: horo2004
Найти производную функции
Приложения:
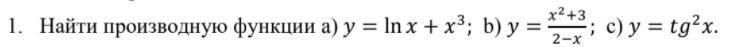
Ответы
Автор ответа:
0
Ответ:
а
б
в
Похожие вопросы
Предмет: Русский язык,
автор: анушкали
Предмет: Окружающий мир,
автор: arinaanfimova
Предмет: Английский язык,
автор: ччряггы
Предмет: География,
автор: Xedzhaim
Предмет: Математика,
автор: bozhko505