Предмет: Геометрия,
автор: FantyFly
Задание 6.
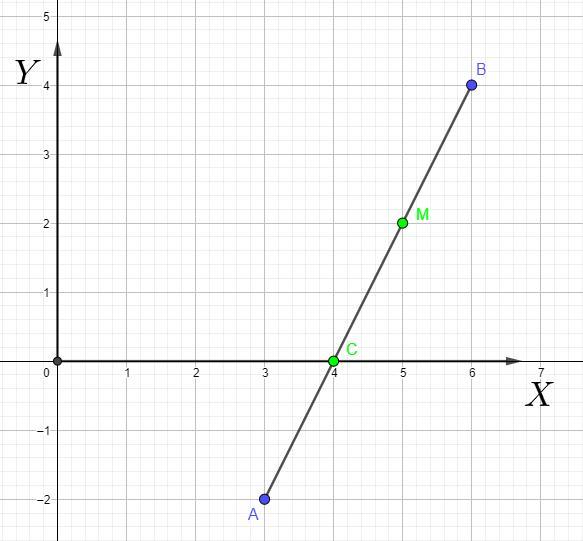
Отрезок с концами в точках А(3;-2) и В(6;4) разделен на три
равные части. Найти координаты точек деления.
Ответы
Автор ответа:
2
Ответ:
Точки C(4;0) и M(5;2) делят отрезок AB на 3 равные части
Объяснение:
Координаты точек A, B согласно условию:
Так как отрезок AB разделен на три равны части, то точки деления будут делить отрезок AB в отношении 1 : 2 и 2 : 1. Вычислим координаты соответствующих точек (смотрите приложение).
Пусть точка C делит отрезок в отношении 1 : 2.
Пусть λ = 1 : 2 = 0,5.
Пусть точка M делит отрезок в отношении 2 : 1.
Пусть λ = 2 : 1 = 2.
То есть точки C и M делят отрезок AB на 3 равные части.
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: Mariuka11
Предмет: Английский язык,
автор: танаев
Предмет: Русский язык,
автор: sev23
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним