Предмет: Математика,
автор: freedom764
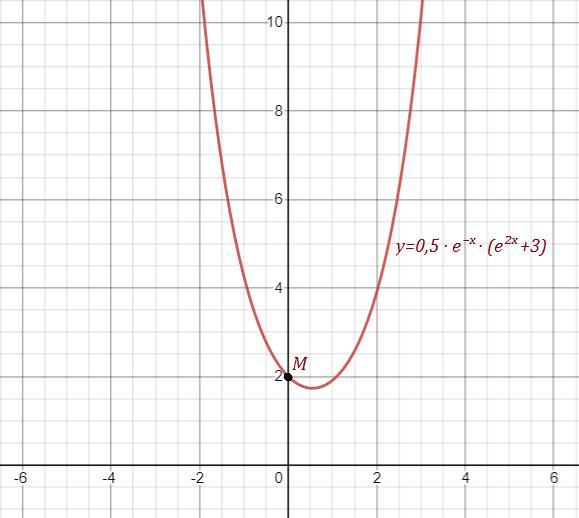
Дано уравнение y'+y=e^x. Найдите интегральную кривую данного уравнения, проходящую через точку (0; 2)
Ответы
Автор ответа:
0
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: maria52002
Предмет: Русский язык,
автор: kusrik
Предмет: Русский язык,
автор: bikamaeva82
Предмет: Информатика,
автор: Тенгерене
Предмет: Геометрия,
автор: Chyvak932