Предмет: Алгебра,
автор: kostik68
Решить диферинциальное уравнение
Приложения:
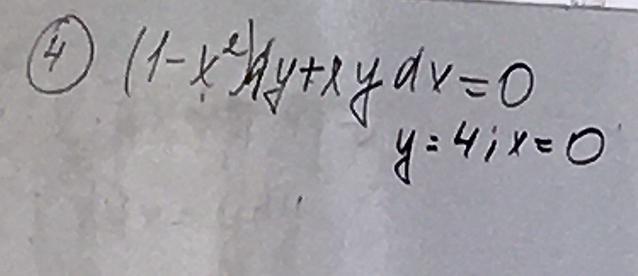
Ответы
Автор ответа:
2
Ответ:
общее решение
частное решение
Похожие вопросы
Предмет: Английский язык,
автор: Chekrai
Предмет: Английский язык,
автор: evgeniyasal
Предмет: Другие предметы,
автор: valertonoyan
Предмет: Математика,
автор: HITR228PIP11
Предмет: Физика,
автор: lnka1367