Предмет: Математика,
автор: sashaesir
Розв’язком якого з рівнянь
Приложения:
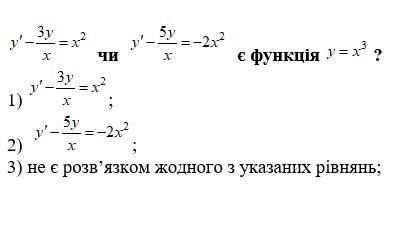
Ответы
Автор ответа:
0
Ответ: 2)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: y7023496441
Предмет: Русский язык,
автор: неважно28
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: chirova84