Question

решите квадратные неравенства x2-9>=0​

Answer 1

Ответ:

( -∞; -3] ∪[3; +∞) - решение квадратичного неравенства

Объяснение:

Решим квадратичное неравенство.

$x^{2} -9\geq 0$

Разложим левую часть неравенства на множители, применяя формулу сокращенного умножения

$a^{2} -b^{2} =(a-b)(a+b)$

$x^{2} -3^{2} \geq 0;\\(x-3)(x+3)\geq 0$

Рассмотрим функцию $f(x)=(x-3)(x+3)$

Область определения функции $D(f)=$ ( - ∞ ; +∞ )

Найдем нули функции, решив уравнение $f(x)=0$

$x{_1}=3;x{_2}= -3$

Нули функции разбивают область определения на 3 промежутка, в каждом из которых функции непрерывна, не обращается в нуль, а значит сохраняет свой постоянный знак.

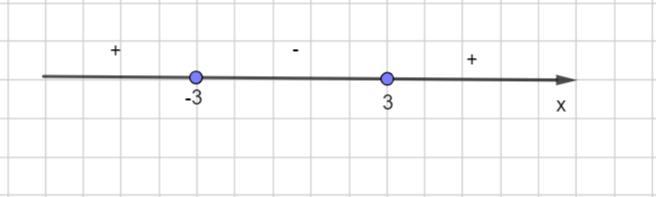
Определим знак функции на каждом промежутке ( рисунок во вложении)

$f(x)\geq 0$  при  х∈ ( -∞; -3] ∪[3; +∞)