Предмет: Геометрия,
автор: kramarenkopolina724
Решите задачу, с рисунком
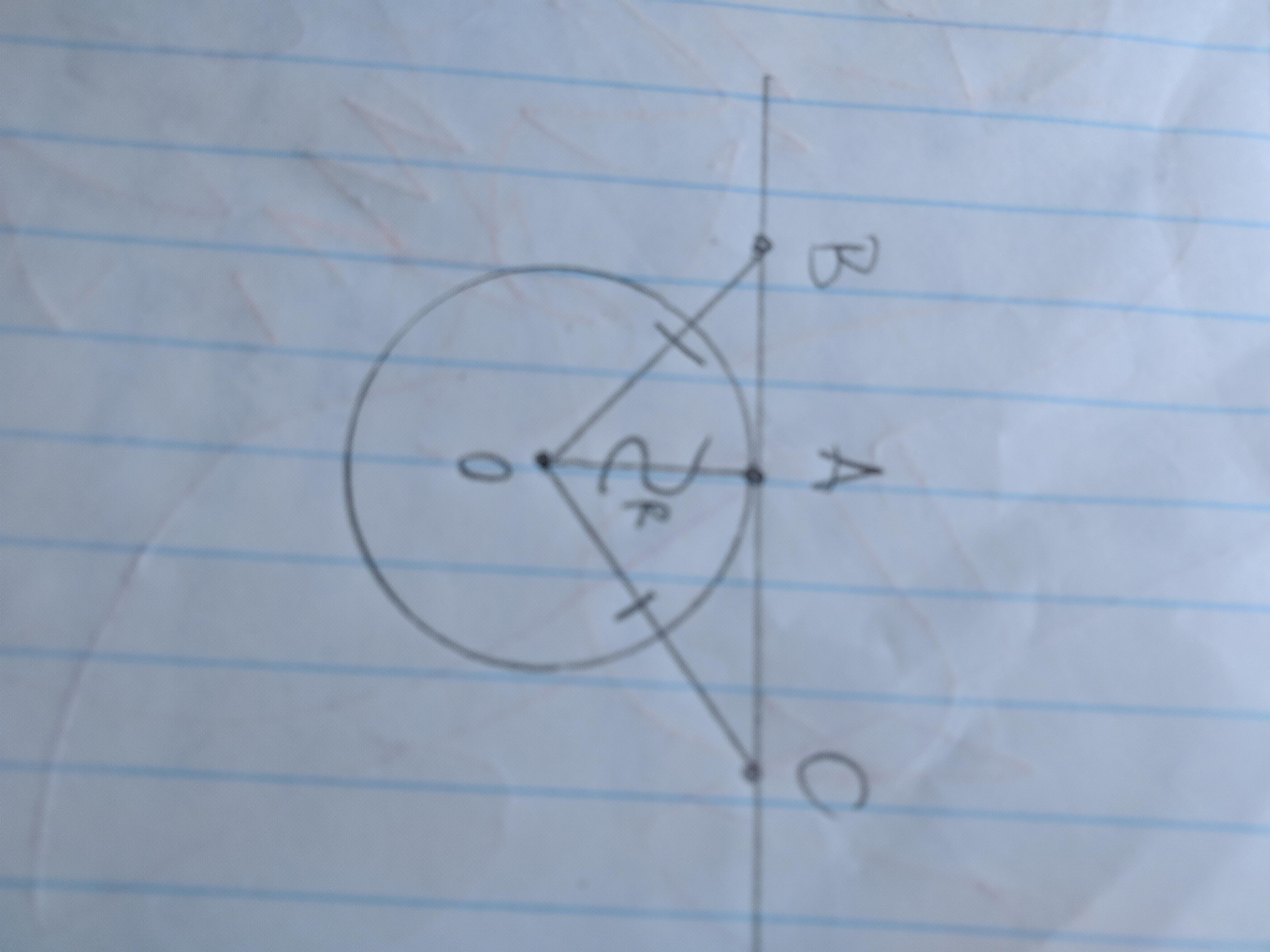
Прямая касается окружности с Центром О в точке А. на касательной по разным сторонам от точки A отмечены точки В и С такие, что ОВ=ОС. Докажите что ВА=АС
Ответы
Автор ответа:
2
Ответ:
Объяснение:
ΔАВО,ΔАСО-прямоуг.т.к. АО=R ⊥ касс-ВС
ΔАВО=Δ.АСО т.к.
1.АО-общ
2.ВО=ОС-по усл.
По катету и гип.
Из рав.-ва Δ-ков ⇒рав.-во сторон. ВА=ВС ч.т.д.
Приложения:
kramarenkopolina724:
Рисунок нужен
Похожие вопросы
Предмет: Русский язык,
автор: aleks79174325616
Предмет: Русский язык,
автор: рараммиаим
Предмет: Русский язык,
автор: тусинка
Предмет: Алгебра,
автор: almazovsyimyk
Предмет: Алгебра,
автор: MiracleOne