Предмет: Геометрия,
автор: vdariisd
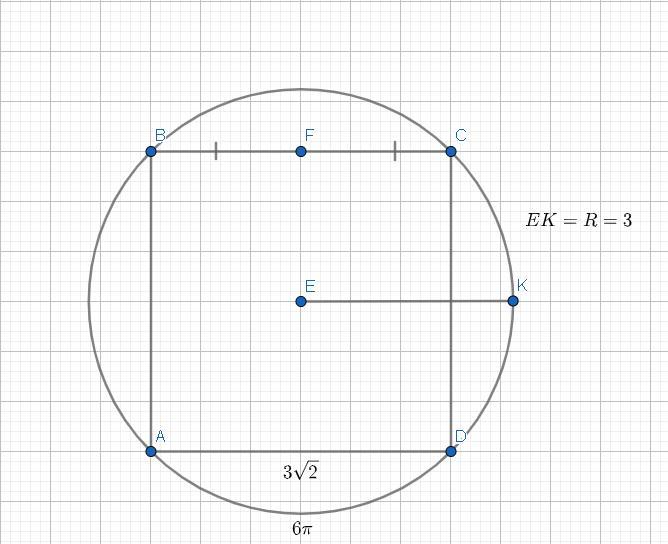
Даны две окружности, вписанная и описанная около квадрата. Длинна большей окружности 6п. Найти площадь квадрата
Ответы
Автор ответа:
1
Площадь квадрата равна квадрате его стороны.
Нам известна длина описанной окружности, если мы найдём её радиус, то сторону квадрата мы вычислим по такой формуле:
Формула вычисления радиуса окружности, зная его длину:
Вернёмся к первой формуле:
Что означает, что:
То есть так получилось, что наличие вписанной окружности нам не пригодилось в решении задачи.
Вывод: S = 18е.д.².
Приложения:
Похожие вопросы
Предмет: Французский язык,
автор: Аноним
Предмет: Английский язык,
автор: kamilyanurmieva
Предмет: Русский язык,
автор: usersamung3421
Предмет: История,
автор: vp03102004
Предмет: Русский язык,
автор: enastay1998