Предмет: Геометрия,
автор: MARIMUR280305
Помогите, очень срочно надо!
Длина окружности, вписанной в равнобокую трапецию, равна 12π см. Найдите площадь трапеции, если ее боковая сторона равна 13 см
С рисунком пожалуйста!!
Ответы
Автор ответа:
3
Ответ:
Площадь трапеции S=156 см²
Объяснение:
Окружность можно вписать в трапецию тогда и только тогда, когда сумма ее боковых сторон, равна сумме оснований т,е AB+CD= AD+BC
13+13=26см ( AD+BC ), отсюда - сумма оснований AB+CD=26см,
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=(а+b):2*h
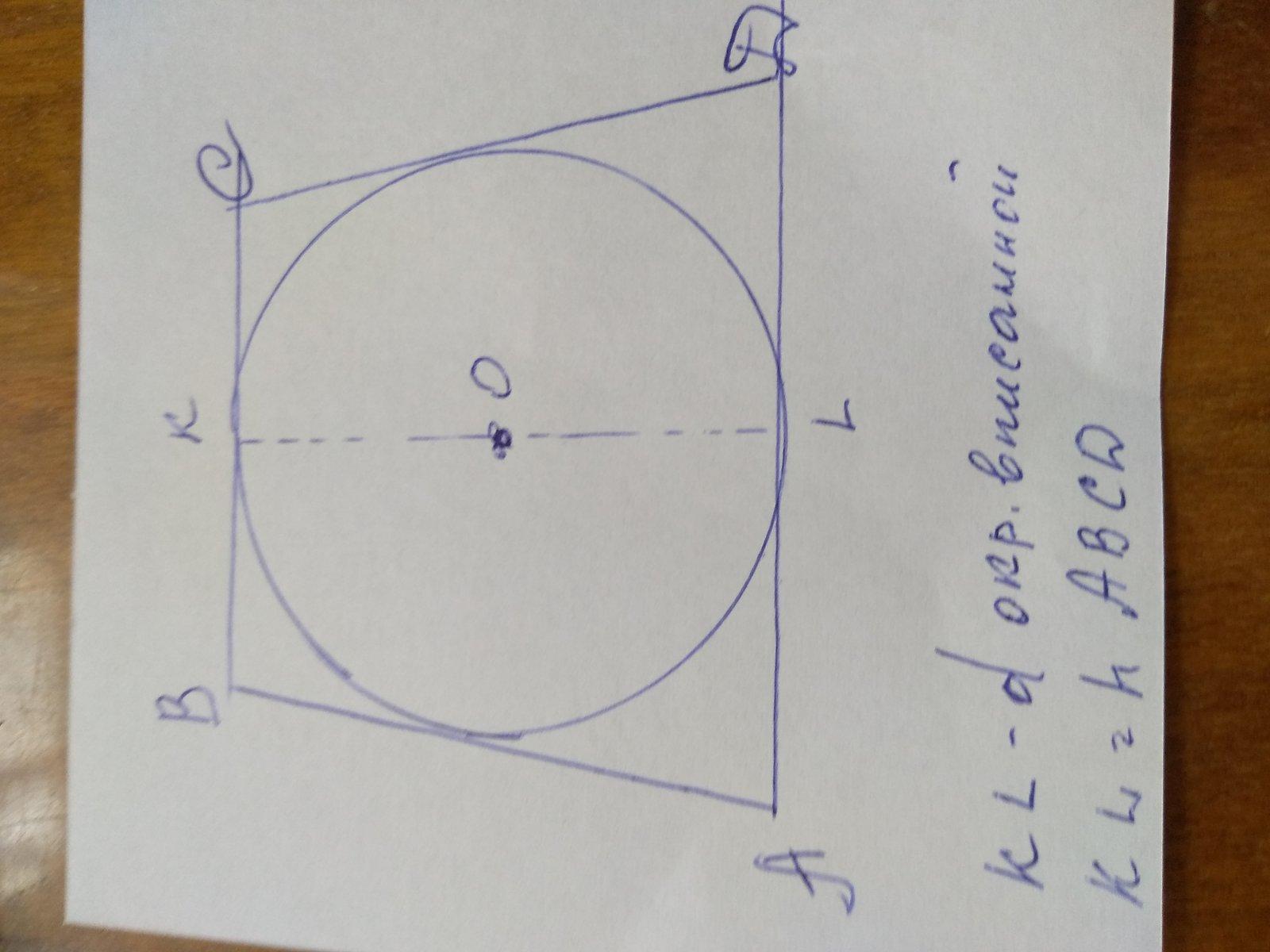
Высота равнобокой трапеции АВСD равна диаметру вписаной окружности. Зная длинну вписанной окружности в трапецию АВСD, найдем ее диаметр по формуле: P=πd , где P-длинна окружности, которая по условию задачи равна 12πсм.
Подставляем известные значения в формулу и находим диаметр:
12π= πd
d =12π:π; d=12см
Площадь трапеции S=26:2*12=156 см²
Приложения:
MARIMUR280305:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: khalitovtimurk
Предмет: Русский язык,
автор: matveikatematve
Предмет: Қазақ тiлi,
автор: dbistaev
Предмет: Математика,
автор: annamarsy
Предмет: Українська мова,
автор: andraynaypakp2x7zf