Предмет: Математика,
автор: vikalunkina
помогите пожалуйста хоть 6-7 примеров
первообразная
Приложения:
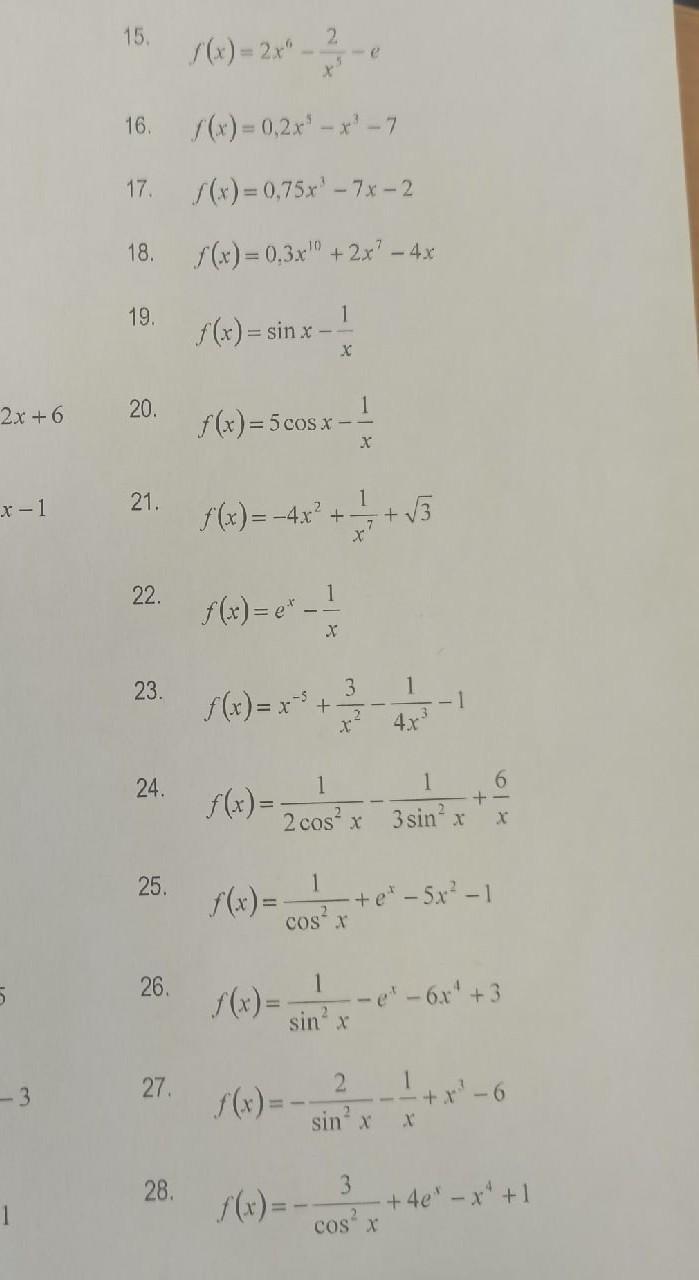
Ответы
Автор ответа:
1
Ответ:
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Похожие вопросы
Предмет: Русский язык,
автор: babinceva1983
Предмет: Русский язык,
автор: alenshik1
Предмет: Українська мова,
автор: Sachasekretnaya1982
Предмет: Английский язык,
автор: natashapanchen
Предмет: География,
автор: sheripat14