Предмет: Алгебра,
автор: maksimkadada
1. Чему равно значение производной функции в точке x0, если
2. Найдите производную функции :
Помогите пожалуйста, друзья.
Приложения:
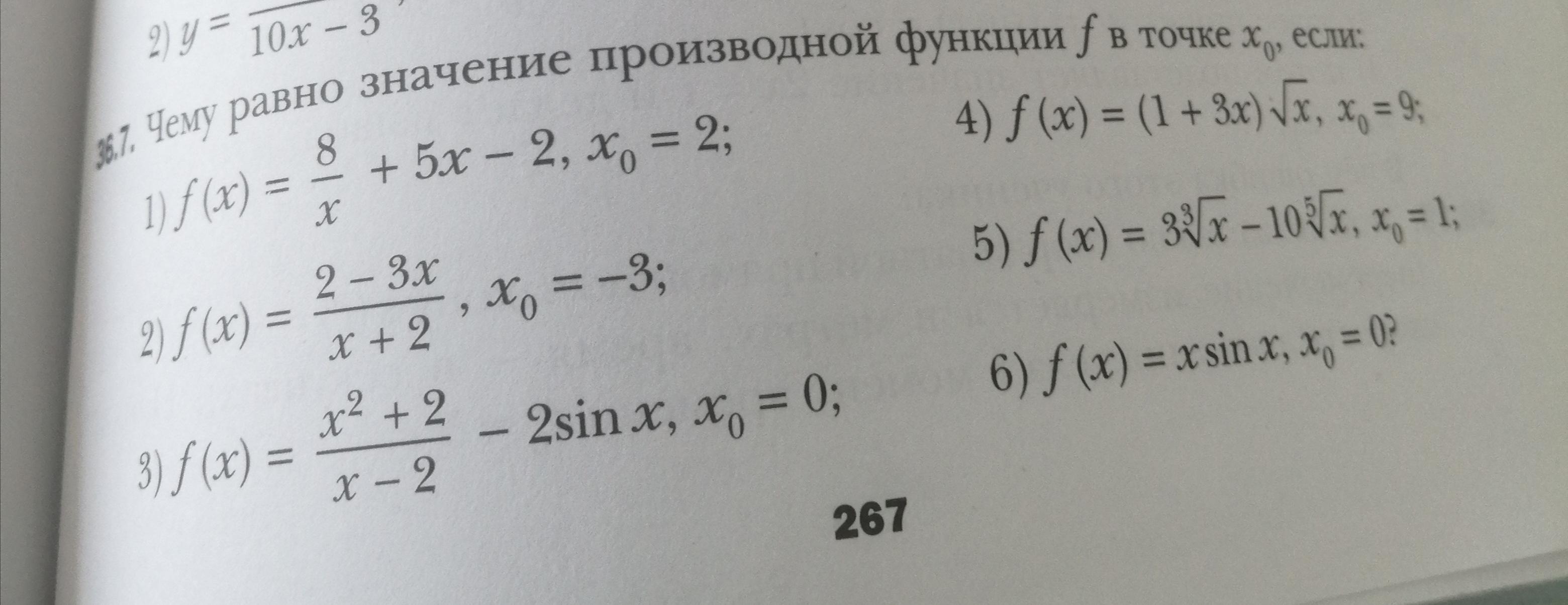
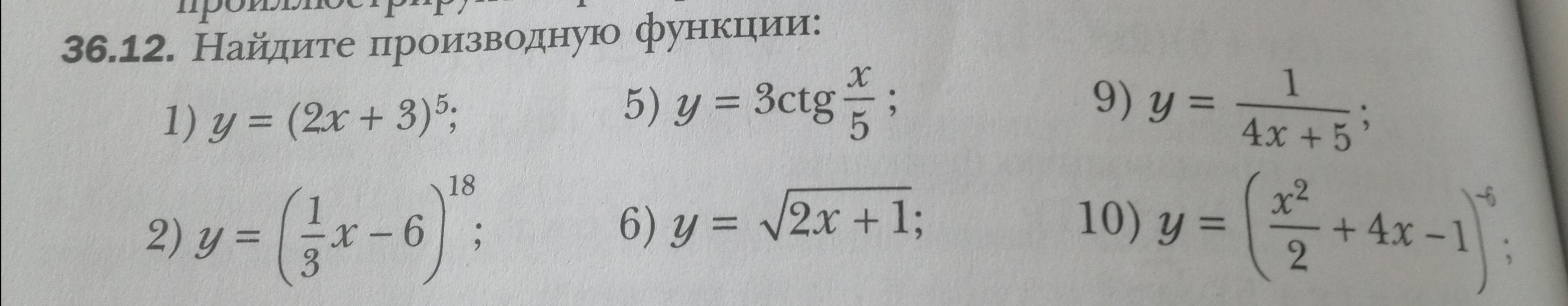
Ответы
Автор ответа:
0
36.7
1
2.
3.
4.
5.
6.
36.12
1
2
5
6
9
10
Похожие вопросы
Предмет: Русский язык,
автор: фонетическийразбор
Предмет: Русский язык,
автор: miralina1
Предмет: Русский язык,
автор: alina061104
Предмет: Физика,
автор: Аноним