постройте график функции y=x^2-4|x|-x и определите, при какиз значениях m прямая y=m имеет с графиком не менее одной, но не более трех общих точек
Ответы
Ответ:
Объяснение:
1) при х≥0 IxI=x
y=x²-4|x|-x=y=x²-4x-x=x²-5x
y=x²-5x графиком этой функции является парабола у которой
ветви направлены вверх так как коэффициент при х² равен 1 и 1≥0
абсцисса вершина параболы х₀=-b/2a=-(-5)/2=2,5
ордината вершины параболы у₀=у(х₀)=(2,5)²-5*2,5=-6,25
найдем абсциссы точек пересечения с ОХ
y=x²-5x =x(х-5) =0 х₁=0 ;x₂=5
2) при х<0 IxI=-x
y=x²-4|x|-x=y=x²+4x-x=x²+3x
y=x²+3x графиком этой функции является парабола у которой
ветви направлены вверх так как коэффициент при х² равен 1 и 1≥0
абсцисса вершины параболы х₀=-b/2a=-3/2=-1,5
ордината вершины параболы у₀=у(х₀)=(-1,5)²+3(-1,5)=2,25-4,5=-2,25
найдем абсциссы точек пересечения с ОХ
y=x²+3x =x(х+3) =0 х₁=0 ;x₂=-3
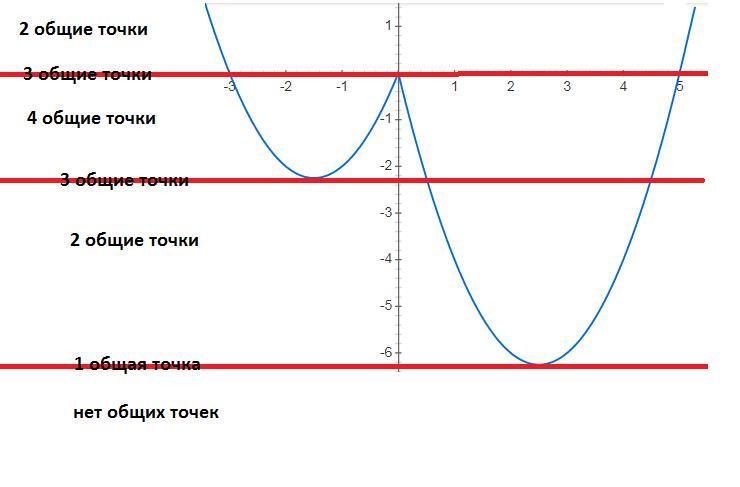
рассмотрим различные расположения прямой у=m
а) при m< -6,25 прямая y=m не имеет с графиком y=x^2-4|x|-x общих точек
б) при m=-6,25 прямая y=m имеет с графиком y=x^2-4|x|-x одну общую точку
в) при -6,25<m<-2,5 и 0<m прямая y=m имеет с графиком y=x^2-4|x|-x две общие точки
г) при m=-2,25 и m=0 прямая y=m имеет с графиком y=x^2-4|x|-x три общие точки
д) при -2,25<m<0 прямая y=m имеет с графиком y=x^2-4|x|-x четыре общие точки, эта область нам не подходит
таким образом прямая y=m имеет с графиком не менее одной, но не более трех общих точек
при m -6,25≤m≤-2,25 и m≥0
m∈[-6,25;-2,25]∪[0;+∞)